作業姿勢評価のための生体力学モデル
【1】概要
人がある姿勢で作業をする場合、自分の姿勢を維持するために筋力を使う。取り扱い物や操作力がある場合も、それに応じた筋力を発揮して作業する。同じ質量や同じ操作力であっても、姿勢が変われば負担感や負担部位は変わる。これは姿勢に応じて発揮する筋力や使用する筋が変わるためである。
これらの問題を扱うには、人の姿勢や動作および取り扱い物や操作力との関係を力学的なモデルで表して評価する生体力学 (Biomechanics) が利用される。作業姿勢を生体力学的にとらえると、なぜこの姿勢が負担になるのか、なぜこの作業条件では負担が高くなるのか、どうすれば負担を軽減できるのかを理論的に理解できる。つまり生体力学は、姿勢や動作の人間工学評価法に理論的な裏付けを与える。
以下に、関節モーメントと腰部椎間板圧縮力により姿勢の負担や腰部への負担をシンプルな生体力学モデル(静的な2次元モデル)で評価する方法を示す。前者はなぜ荷物は体に近いところで持たなければならないのかという疑問、後者はなぜ前傾姿勢で荷物を持ってはならないのかという疑問に答えるものである。多くの評価ツールの理論的背景や評価の数値化は、これらのモデルをベースにしている。
【2】上肢の荷物保持における生体力学モデル
1)前腕が水平な場合の肘関節モーメント
下図に示すように、人が前腕を水平にして質量mの荷物(10 kg)を手の位置で保持しているとする。この時、肘関節まわりに荷物質量mによるモーメントM0と腕(手+前腕)の質量m1によるモーメントM1が時計回りに発生している。この状態で腕が下がらないためには、肘関節の上腕二頭筋などの屈筋群が働いて、反時計回りのモーメントMを発揮してつり合いをとる必要がある。
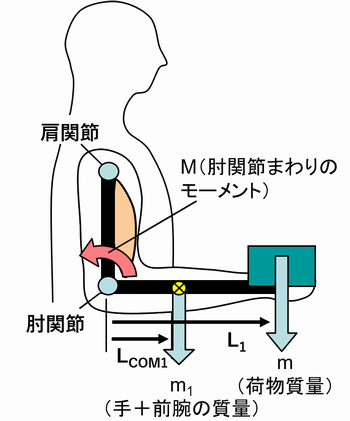
ここで、人の身長を1.7 m、体重を65 kgとし、手と前腕を合わせた長さ(手・前腕長)は身長の0.20倍、質量は体重の0.020倍(片腕分)、重心位置は肘関節から0.53×(手・前腕長)とすると各部の長さや重さは以下のようになる。
荷物から肘までの距離L1=手・前腕長=0.34 m(=0.20×1.7)
腕(手+前腕)の質量m1=1.3 kg(=0.020×65)
腕の重心位置から肘までの距離LCOM1=0.1802 m(=0.53×L1)
以上の値を用い、肘関節まわりの荷物の質量によるモーメントM0および腕の質量によるモーメントM1を求めると以下のようになる(gは重力定数=9.8 m/s2)。
M0=m×g×L1
M1=m1×g×LCOM1
従って、腕を保持するのに必要な筋力によるモーメントM(Nm)は次式で示される。
M = M0+M1=m×g×L1+m1×g×LCOM1
=(m×L1+m1×LCOM1)×g ―――――――――― (1)
=(10×0.34+1.3×0.1802)×9.8=35.6 Nm
2)前腕が斜めの場合の肘関節モーメント
次に下図の通り、前腕が斜めにθ1傾いている場合を考える。
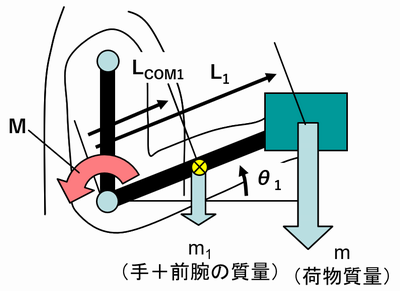
この場合、肘関節まわりの荷物によるモーメントM0および腕の質量によるモーメントM1はそれぞれ以下の式で示される。
M0=m×g×L1×cosθ1
M1=m1×g×LCOM1×cosθ1
従って、腕を保持するために必要な筋力によるモーメントM (Nm)は次式で示される。
M = M0+M1=m×g×L1×cosθ1+m1×g×LCOM1×cosθ1
=(m×L1+m1×LCOM1)×g×cosθ1 ―――――――― (2)
式(2)は、単純に前の式(1)にcosθ1が付いただけである。前述と同じ体格等の状況でθ1が30°とすると、
M =(m×L1+m1×LCOM1) ×g×cosθ1
=(10×0.34+1.3×0.1802)×9.8×cos30°
=30.8 Nm
式(2)を見るとわかるように、θ1が0°、つまり前腕を水平に保った状態がMは最大になり、θ1が-90°の時、つまり前腕を真下に垂らした状態ではMは0 Nmで最少になる。θ1が+90°の時もMは0 Nmになって最少になる。人が手で荷物を運ぶ際に腕を真下に下げる(θ1=-90°)のは、肘関節のモーメントを小さくして楽な姿勢を選んでいることになる。ただし大きな荷物や手提げ袋などでは、腕を真下に下げると荷物が足に引っかかったり地面に触れたりして歩きにくくなる。その場合は、上腕は下垂したままで肘をできるだけ曲げて前腕を真上に向けた姿勢で荷物を持とうとする(θ1を+90°に近づける)。これも肘関節のモーメントが小さな姿勢のためである。
3)肩関節モーメント計算への拡張
前述の肘関節のみのモデルを拡張し、肩関節のモーメントを求めてみる。下図に示すように、腕を前方に挙上した姿勢で荷物を片手で保持しているとする。
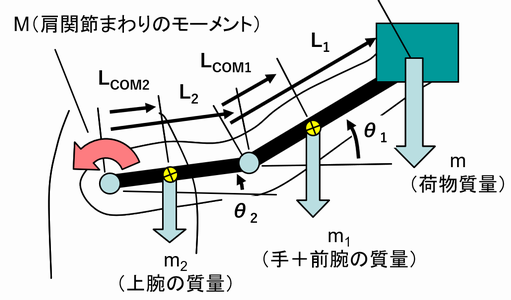
この場合、肩関節まわりのモーメントMは、荷物による肩関節まわりのモーメントM0、前腕質量による肩関節まわりのモーメントM1、上腕質量の肩関節まわりのモーメントM2の3つのモーメントの和になる:
M=M0+M1+M2
ここで、M0、M1、M2はそれぞれ次式のようになる。
M0=m×g×(L1×cosθ1+L2×cosθ2)
M1=m1×g×(LCOM1×cosθ1+L2×cosθ2)
M2=m2×g×LCOM2×cosθ2
つまりMは、以下のようになる。
M=m×g×(L1×cosθ1+L2×cosθ2)
+m1×g×(LCOM1×cosθ1+L2×cosθ2)
+m2×g×LCOM2×cosθ2 ―――――――― (3)
前述と同じにように身長1.7m、体重65 kgの人が片手で荷物(m=10 kg)を支えるとする。前腕のパラメータは前述の値を用い、上腕については、長さは身長の0.17倍, 質量は体重の0.029倍(片腕分)、重心位置は肩関節から0.44×上腕長とすると、m1=1.3 kg、m2=1.885 kg(=0.029×65)、L1=0.34 m、L2=0.289 m(=0.17×1.7)、LCOM1=0.1802 m、LCOM2=0.12716 m(=0.44×L2)となる。ここでθ1=30°、θ2=10°とすると、肩関節のモーメントMは以下のように求められる:
M=m×g×(L1×cosθ1+L2×cosθ2)
+m1×g×(LCOM1×cosθ1+L2×cosθ2)
+m2×g×LCOM2×cosθ2
=10×9.8×(0.34×cos30°+0.289×cos10°)
+1.3×9.8×(0.1802×cos30°+0.289×cos10°)
+1.885×9.8×0.12716×cos10°
=56.75+5.61+2.31
=64.7 Nm
ちなみに、肘関節のモーメントは、前に求めた時と前腕の傾き角などの条件が同じなので30.8 Nmである。
式(3)は変数が多いので少しわかりにくいが、θ1=θ2=0°の時(腕をまっすぐ前に伸ばした姿勢)で肩・肘両方の関節モーメントがいずれも最大となる。また、θ1=-90°かつθ2=-90°(腕をまっすぐ下に垂らした状態)あるいはθ1=+90°かつθ2=-90°(上腕を下垂し、前腕を真上にあげた姿勢)に近い姿勢では、荷物と肩・肘関節との水平距離がいずれも近くて両方の関節モーメントとも0 Nmに近くなるので楽な姿勢になる。θ1=+90°かつθ2=+90°(腕をまっすぐ上にあげた姿勢)でも肩・肘の関節モーメントは同様に 0 Nmになるが、真上に伸ばした手で重い荷物を持ってバランスをとるのは難しく、かつ肩関節は最大可動域に近くて維持しにくい姿勢なので、通常は採用されない姿勢である。
上記の手順で体節(セグメント)を、体幹(頭部、頸部、胸部、腹部、腰部)、大腿、下腿、下腿、足部と増やしていけば、全身の関節の2次元のモーメントが計算できる。
4)モーメント比による評価
関節モーメントは、値が高いとそれだけ筋発揮が必要で負担になるため、それ自体が評価値として利用できる。姿勢や荷物質量を変えて関節モーメントが低い条件を探せば、改善条件の探索ができる。
ただし、関節によって発揮できるモーメントには大きな差があるので、関節間の負担を比較するには関節の差を標準化する方法が必要である。その1つが、その関節で発揮できる最大モーメントで標準化するというモーメント比による方法である。
ある姿勢でのある関節のモーメントをM、その姿勢でその関節で発揮できる最大のモーメントをMmaxとすると、モーメント比MRは以下の式で求められる:
MR=M/Mmax×100 (%) ―――――――― (4)
モーメント比MRは、その姿勢で発揮できる最大筋力の何パーセントの筋力を発揮しているかという最大筋力比(%MVC)に相当する値になるので、直感的に理解しやすい。たとえば50%だと最大筋力の半分だから筋血流も停止しかけてかなりきつい、10%だとかなり楽、20~30%なら日常生活レベルなどと想像できる。
最大モーメントは実測する場合もあるが、通常は文献値を利用する。たとえば、肘関節や肩関節の屈曲の最大モーメントについては、文献[1]に以下の式が示されている。
肘関節:Mmax=(336.29+1.544×E-0.0085×E2-0.5×S)×G
ただし、Gは補正係数(男性は0.1913、女性は0.1005).
肩関節:Mmax=(227.338+0.525×E-0.296×S)×G
ただし、Gは補正係数(男性は0.2845、女性は0.1495).
いずれも、Eは肘関節角で [肩関節-肘関節-肘関節] のなす角(まっすぐ腕を伸ばした状態が180°)、Sは肩関節角で [股関節-肩関節-肘関節] のなす角(直立で腕を下垂した状態が0°)である。式にEやSが含まれていることは、これらの関節角により最大モーメントが変わることを示している。
この最大モーメントを利用し、前述の肩関節モーメントと肘関節モーメントを評価してみる。
まず、肘関節と肩関節の最大モーメントを求める。肘関節角Eと肩関節角Sはθ1とθ2より以下のように求められる。
E=180-(θ1-θ2)=180-(30-10)=160°
S=90+θ2=90+10=100°
人を男性とすると、肘関節と肩関節の最大モーメントは以下の通りである:
肘関節最大モーメントMEmax
=(336.29+1.544×E-0.0085×E2-0.5×S)×0.1913
=(336.29+1.544×160-0.0085×1602-0.5×100)×0.1913
=60.40 Nm
肩関節最大モーメントMSmax
=(227.338+0.525×E-0.296×S)×0.2845
=(227.338+0.525×160-0.296×100)×0.2845
=80.15 Nm
この姿勢での肘関節と肩関節のモーメントは、既に求めたとおり以下の値である:
肘関節ME=30.8 Nm
肩関節MS=64.7 Nm.
従って、肘関節と肩関節のモーメント比MREとMRSは以下のようになる。
肘関節 MRE=ME/MEmax×100=30.8/60.40×100=51%
肩関節 MRS=MS/MSmax×100=64.7/80.15×100=81%
両関節のモーメント比も50%を超える高い値となっており、当然ながら、あのような上肢を挙上した姿勢で10 kgの荷物を持ってはならないことがわかる。
(補足)
(1)以上の手続きを踏まえて体節を増やし、全身の各関節についてモーメント及びモーメント比を求めると、その姿勢でどの関節まわりのモーメント比が高くなるか、つまり体のどこの部位に負担を感じる姿勢かを判定できるようになる。
(2)荷物ではなく操作力による力が手や体にかかる場合も、その体節にかかる力をX軸成分とY軸成分に分離して計算すれば、同様な手続きでモーメントが計算できる。
(3)体節が増えて荷物質量だけでなく操作力も扱うようになると、そろそろ位置ベクトルと力のベクトルの外積を利用してモーメントを計算するほうが計算は単純で見通しもよくなる。
(4)上記のモデルは静的(加速度や角速度の影響がゼロとみなすモデル)である。動作が速くなるとずれが大きくなる。ただし、スポーツ場面とは異なり、仕事や生活場面では高い加速や角速度が要求される、つまりスキルやタイミングが要求される作業設計や製品作りは本質的に避けるべきである。
(5)関節は最大可動域付近になると、関節を構成する骨による可動制限や関節周囲にある靭帯による制限あるいは筋自体の長さの制限などから、筋力によらない受動的なトルク成分が発生する。生体力学モデルをより精緻にするには、このような受動成分も適宜モデルに組み込むが、姿勢の設定もあわせて厳密にする必要がある。
【3】腰部負担評価のための腰部椎間板圧縮力推定
職場での訴えとして腰痛は多く、姿勢や荷物質量によって腰部にかかる負担が変わることはよく認識されている。そのため、腰部への負荷を生体力学的に評価する方法もよく利用されている。評価値としては、前述した関節モーメントも利用できるが、L5/S1の椎間板にかかる力(腰部椎間板圧縮力)の推定値もよく利用される。いずれも、腰部の関節としては第5腰椎・仙椎間(以下、L5/S1)でのモーメントや圧縮力が求められる。
人が下図の姿勢で荷物を保持しているとする。
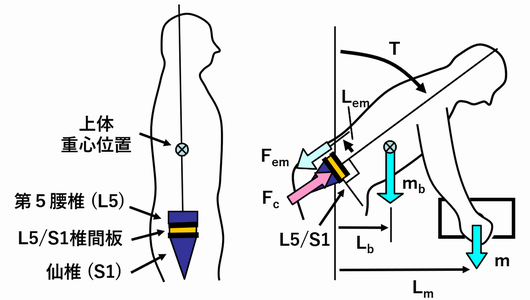
変数は以下のとおり:
m:荷物質量 (kg)
Lm:L5/S1から荷物重心位置までの水平距離 (m)
mb:L5/S1より上の腕も含んだ体(上体)の質量 (kg)
Lb:L5/S1から上体の重心位置までの水平距離 (m)
T:上体の前傾角。直立位を0(度)とする。
Fem:脊柱起立筋筋力 (N)
Lem:脊柱起立筋のモーメントアーム (m)
g:重力加速度(=9.8 m/s2)
腰部椎間板圧縮力Fcは、L5/S1まわりのモーメントのつり合いとL5/S1関節面での力のつり合いの2つの式をたて、その連立方程式を解くことで求められる。
まず、L5/S1まわりのモーメントのつり合いを考える。前の図において、荷物質量mによるモーメントMmと上体質量mbによるモーメントMbはL5/S1のまわりの時計回りのモーメントで、これにつり合うように発生する反時計回りのモーメントが脊柱起立筋の筋力FemによるモーメントMemである。つまり、次のモーメントのつり合いの式が成り立つ。
Mm+Mb=Mem ・・(1)
各モーメントは以下のように求められる。脊柱起立筋のモーメントアームLemは、腰椎椎体中心から脊柱起立筋中心までの前後距離である。
荷物 Mm=m×g×Lm ・・・(2)
上体体重 Mb=mb×g×Lb ・・・(3)
脊柱起立筋 Mem=Fem×Lem ・・・(4)
式(1)に式(2)~(4)を代入すると以下のようになる。
m×g×Lm+mb×g×Lb=Fem×Lem ・・・(5)
次にL5/S1面での力のつり合いを考える。
L5/Sの椎間板を圧縮する力は荷物質量・上体質量・脊柱起立筋筋力の3成分Fcm、Fcb、Fcemの和で、それに対抗して受動的に発生するのが椎間板圧縮力Fcである。つまり、
Fc=Fcm+Fcb+Fcem ・・・(6).
荷物質量mと上体質量mbによる椎間板圧縮力の成分FcmとFchは、L5/S1面を垂直に押す力の成分に限られる。脊柱起立筋筋力Femによる圧縮力Fcemは、筋線維がL5/S1関節面に平行に走行していることからすべての力の成分が圧縮力として作用するとする。従ってFcm、Fcb、Fcemの3つの成分は以下のように表せる:
Fcm=m×g×cos T ・・・(7)
Fcb=mb×g×cos T ・・・(8)
Fcem=Fem ・・・・・・(9)
式(6)に式(7)~(9)を代入すると以下のようになる:
Fc=m×g×cos T+mb×g×cos T +Fem ・・・(10).
結局、式(5)と式(10)の連立方程式をFemとFcについて解くことになる。
つまり式(5)より脊柱起立筋筋力Femは、
Fem=(m×g×Lm+mb×g×Lb)/Lem ・・・(11)
なので、これを式(10)に代入するとFcは以下のように求められる:
Fc=m×g×cos T+mb×g×cos T + (m×g×Lm+mb×g×Lb)/Lem
=m×g×( cos T+Lm/Lem)+mb×g×( cos T+Lb/Lem)・・・(12)
計算例)
以下の条件で実際の腰部椎間板圧縮力を求めてみる。
m=20 kg:荷物質量
Lm=0.60 m:荷物の重心位置からL5/S1までの水平距離
mb=35 kg:上体の質量
Lb=0.30 m:上体の重心からL5/S1までの水平距離
T=60°:上体の前傾角
Lem=0.065 m:脊柱起立筋のモーメントアーム長 [1]
g=9.8m/s2:重力加速度
この条件での腰部椎間板圧縮力Fcは、式(12)に各値を代入して、
Fc=m×g×(cos T+Lm/Lem)+mb×g×(cos T+Lb/Lem)
=20×9.8×(cos 60°+0.60/0.065)+35×9.8×(cos 60°+0.30/0.065)
=1907.2+1754.6
=3662 N
一般的な腰部椎間板圧縮力Fcの限界値としては、3,400 Nという値が広く利用されている。この条件では腰部椎間板圧縮力Fcは3,662 Nと推定され、椎間板圧縮力の許容限界値である3,400 Nより大きい。従って、今回の作業条件は腰痛の発症リスクがあると判定される。
上記の式(12)は、変数が多くて腰部椎間板圧縮力Fcと上体の前傾角Tとの関係をとらえにくい。そこで、荷物はまっすぐ下に垂らした腕で肩の真下で保持すると仮定すると、荷物の水平距離Lmと上半身重心の水平距離Lbは前傾角Tの正弦 (sin T) に比例する値になる。この関係を式(12)に組み入れると、腰部椎間板圧縮力FcはTのみを変数とする式で表わせる。この場合、Tがおおむね0~80°の範囲だとFcは上に凸のサインカーブで単調に増加する。つまり、体が前傾するほど腰部負担が上がって腰への負担が高くなることを単純に示すことができる。
(補足)
(1)上記のモデルは、前かがみで荷物を持って姿勢を保持する条件なので時計周りのモーメントを支えるために反時計まわりのモーメントを発生することができる脊柱起立筋の筋力で計算している。これに対して立位で肩の高さで台車を前に押す作業の場合では、台車の押し力が反時計周りのモーメントを生じるので、これを支えるには時計回りのモーメントが発揮できる腹直筋の筋力で計算する必要がある。その場合は、筋のモーメントアームも脊柱起立筋から腹直筋に変更することになる。腹直筋のモーメントアームは脊柱起立筋より長いので、筋力によるL5/S1関節面を押す成分は減少し、腰部椎間板圧縮力Fcも低めになる。それゆえ、台車は引くより押すほうが安全と言われることもある。ただしSnookのテーブルあるいはLM-MMH式で見る限り、実際の押し引き動作では押すと引くでは同じか押すほうがやや高い。
(2)腰部には多数の筋(腸腰筋、大腰筋腰、方形筋、広背筋、外腹斜筋、内腹斜筋など)があるので、厳密にいえば腰部のモーメントは腰周囲の多数の筋の筋力でつり合うようになっている。その場合、個々の筋力を実測することはできないので、生体力学モデルでは最適化を用いて筋力の配分する。これにより、より正確に椎間板圧縮力のような関節間力の推定が可能になる。
(3)腰部に限らず多くの関節では、1つの自由度の回転動作にも複数の筋が関与している。これを考慮して厳密に生体力学モデルを組み上げたのが筋骨格モデルである。ただし、上記の例のように1自由度を1つの筋の活動に対応させる単純化したモデルでも、作業場面の人間工学評価においては十分に対応できることが多い。たとえば文献[2]では、6種類の腰部椎間板圧縮力推定モデルの比較を作業現場で多くみられる22種類の作業姿勢で行っている。6種類のモデルのなかには、シンプルなモデルとしては本サイトでも公開しているUBSのUtahのHCBCFの腰部椎間板圧縮力モデル(構成は上記の推定モデルとほぼ変わらない)、オーソドックスな3Dモデルとしては3D SSPP、精密な3次元モデルとして筋骨格モデルであるAnyBodyがあるが、上記3つの腰部椎間板圧縮力推定値の相関係数は0.98以上と非常に高い値と報告されている。つまり、荷物取り扱い作業に限定すればかなりシンプルなモデルでも十分役に立つことがわかる。
文献
[1] Chaffin DB, et al., 0ccupational Biomechanics, 4th edition, Wiley InterScience, 2006
[2] Mohammad Ali Rajaee, Navid Arjmand, Aboulfazl Shirazi-Adl, André Plamondon, Hendrik Schmidt, Comparative evaluation of six quantitative lifting tools to estimate spine loads during static activities, Applied Ergonomics, Vol. 48, p.22-32, 2015, https://doi.org/10.1016/j.apergo.2014.11.002