NIOSHの荷物持ち上げ式 (NIOSH lifting equation, NLE)とISO 11228-1 (JIS Z8505-1) の持ち上げの概要
【1】はじめに
【2】NLEの単一タスク解析:RWLとLI
【3】NLEの各乗数等の概要
【4】NLEの複数タスク解析(複合持ち上げ指数CLI)
【5】その他の複数タスク解析法
【6】作業設計や作業改善への利用
【7】NLEの計算例
【8】ISO 11228-1 (JIS Z8505-1) の持ち上げ
【9】持ち上げ指数LIの解釈の再検討
【10】適用範囲
【11】適用場面の例
参考文献
(補足説明1)なぜ、NLEには作業姿勢の要因が含まれていないのか
(補足説明2)なぜNLEの負荷定数LCは23 kgなのか
【1】はじめに
NIOSHの荷物持ち上げ式(以下、NLE)は、荷物取扱い作業による腰痛予防を目的とした作業評価や作業設計を支援するために作られたものである [1]-[4]。荷物取扱い作業に伴う健康障害を防ぐには、取扱い重量や取扱い回数だけでなく、荷物の取扱い位置・持ち上げ距離・体のひねり・荷物の持ち易さなど多くの要因を考慮する必要がある。NLEは、荷物取扱いに関する生理学・心理物理学(精神物理学)・生体力学・疫学の各分野での研究成果を統合して作られたものである。
NLEの成果を踏まえ、さらに適用範囲を広げたのがISO 11228-1 (JIS Z8505-1)の持ち上げの評価法である[5]-[6]。
この資料では、まずNLEの概要を説明し、それを踏まえてISOの持ち上げ式の簡単な説明を行う。
(注意)以下の【2】~【4】および【10】は、文献[2]の要点をまとめたものである。詳細は文献[2]を参照のこと。
【2】NLEの単一タスク解析:RWLとLI
NLEには、ほぼ同一の条件の荷物取り扱い作業を行う場合の解析(単一タスク解析, Single-task analysis)と、条件の異なる荷物取り扱い作業を何種類実施する場合の解析(複数タスク解析, Multi-task analysis)とがある。ここではまず単一タスク解析の方法を解説する。
単一タスク解析では、まず荷物の持ち上げ距離や持ち上げ頻度などの作業条件からRWL (Recommended Weight Limit, 推奨質量上限)という数値を計算する。このRWL (単位:kg)は、健康な作業者がその作業条件で作業を最大8時間続けても腰痛の発症リスクが増大しないという取扱い質量の限界値である。RWLは、以下の式で計算する。各乗数は次節で説明する。
RWL=LC×HM×VM×DM×AM×FM×CM
ここで、LCは負荷定数、HMは水平乗数、VMは垂直乗数、DMは距離乗数、AMは非対称乗数、FMは頻度乗数、CMは結合乗数である。
RWLが求められたら、次に次式でLI (Lifting Index, 持ち上げ指数)を求める。
LI=L/RWL
ここでLは実際の作業で取り扱う荷物の質量 (Load weight)である。LIは、式が示すように実際の作業が推奨上限であるRWLの何倍になるかを示す値である。結局Lが、与えられた作業条件での荷物取り扱い作業の上限質量であるRWLを越えている、つまりLIが1より大きくなることは、腰痛の発症リスクが高いことを示す。そこで、LIが1.0以下になるように作業設計を行うことが求められる。
【3】NLEの各乗数等の概要
1.LC (Load Constant,負荷定数)
RWLを計算する上での定数で、23 kgとする。他の乗数HM, VM, DM, AM, FM, CMは全て0~1の範囲を取るので、結局、本法ではいかなる場合もRWLは23 kgを越えないことを要求していることになる。
2.HM (Horizontal Multiplier, 水平乗数)
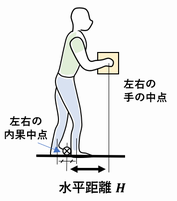
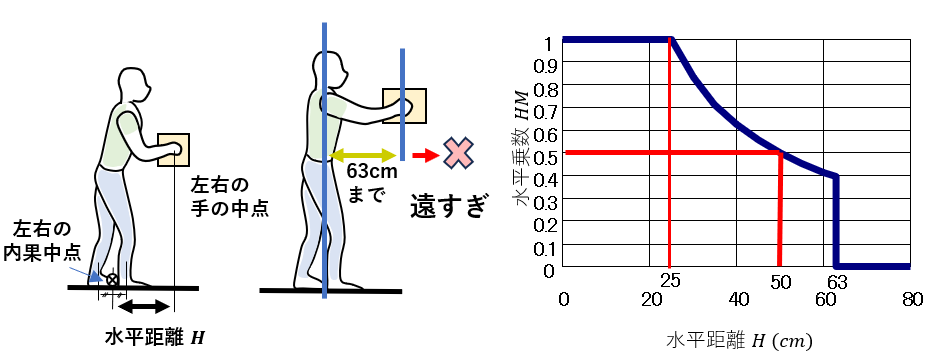
足位置から荷物を保持している手位置までの水平距離H (Horizontal Location,水平位置. 単位:cm)から次式を用いて求める。なお、足位置は足首の位置とし、足が前後している場合は左右の足首(正確には内果)の位置の中点を足位置とする。手位置は握りの位置とし、左右の手位置が異なる場合は左右の手位置の中点を用いる。
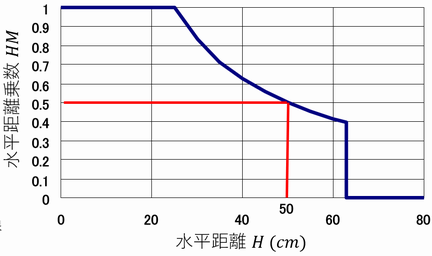
HM = 1 (H≦25 cm)
= 25/H (25cm<H≦63 cm)
= 0 (H>63 cm)
注1)NLEは両手での荷物取扱い作業のみを対象としている。
注2)25 cmは体の幅、63 cmは腕の水平リーチである(男性のみだとこれより遠いところまでリーチできるが、両手での荷物保持や転倒防止を考慮して25インチ、つまり63 cmまでにしている)。
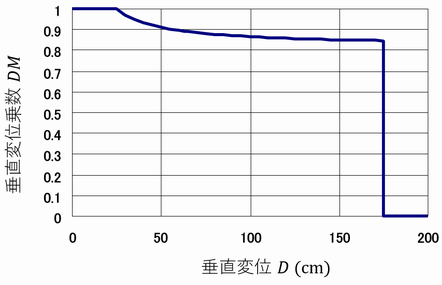
3.VM (Vertical Multiplier,垂直乗数)
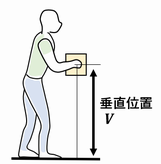
床から荷物を保持している手位置までの垂直距離V (Vertical Location, 垂直位置. 単位: cm) から次式を用いて求める。なお、手位置はHMの場合と同様に定義する。
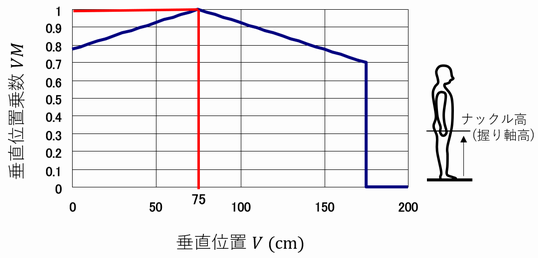
VM = 1-(0.003×|V-75|) (0≦V≦175 cm)
= 0 (V<0 cmまたはV>175cm)
注)75 cmはナックル高(おおむね男女平均のナックル高に相当)、175 cmは上方向の最大リーチ(175 cmは70インチで、おおむね男性の平均身長に相当)である。
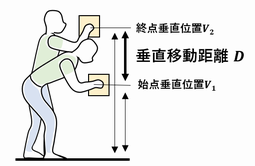
4.DM (Distance Multiplier,距離乗数)
荷物を持ち上げるあるいは下げる垂直方向の移動距離の絶対値D (Vertical travel distance, 垂直移動距離. 単位: cm) から次式を用いて求める。なお、垂直移動距離Dは荷物の始点(移動元)と終点(移動先)の位置での垂直位置Vの差の絶対値である。
DM = 1 (D≦25 cm)
= 0.82+4.5/D (25<D≦175 cm)
= 0 (D>175 cm)
注1)本法では、持ち上げと持ち下げの区別をしない。つまり、始点と終点のどちらが高い垂直位置でもよい。
注2)本法は、非常に速い持ち上げ動作(おおよそ1秒以内に75 cm以上の距離を上げ下げする動作)や落としたり投げるなどの荷物取扱い動作には適用できない。
注3)25 cmは持ち上げの最小幅、175 cmは上方向の最大リーチである。
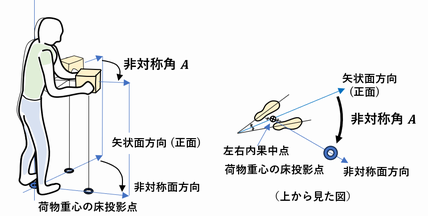
5.AM (Asymmetric Multiplier, 非対称乗数)
荷物が体の正面(矢状面方向)から何度ずれた位置にあるか示す角A(Asymmetry Angle, 非対称角. 単位:度)から次式を用いて求める。非対称角Aは、 床上における両足首中点(正確には左右の内果の中点の床投影点)を角度計測の中心とし、体の正面(矢状面方向)に荷物がある場合を0度、体の真横にある場合が90度になる。
AM = 1-0.0032×A (0≦A≦135度)
= 0 (A>135度)
注1)ここで定義する非対称角Aは荷物の位置を示す値であり、実際の体のひねり量を示す値ではない。
注2)本法における体の正面方向とは、足のかかとから足先への方向ベクトルの左右平均の方向ベクトルの向きである。片足立ちのときは、体重を支えているほうの足を基準とする [*]。
[*] Tomas R. Waters, Chapter 33, Revised NIOSH Lifting Equation, in eds: Amit Bhattachariya, James D. McGlothlin, Occupation Ergonomics – Theory and Application – 2nd ed., CRC Press, NY, 2012, p.894
注3)荷物を始点から終点に動かす際、途中で足を動かして体の向きを変えた場合は、動かした足の方向を体の正面方向として非対称角Aを決める。たとえば始点で体の正面に置かれた荷物を右90度の方向に移動させるとき、足を動かして体全体の向きを右に90度回転させて体の正面で荷物を置いたなら、終点での非対称角Aは0度になる。
注4)非対称角Aは荷物の位置を基に決めるので、荷物重心の床投影点が参照されている。これに対して水平距離Hや垂直位置Vは両手中心位置(あるいはその床投影点)を参照するので、厳密にいえば両者の床投影点の位置はずれる場合がある。ただし、極端に重心が偏った荷物を扱う場合や左右の手を非対称に使用している場合を除けば、荷物重心位置と両手中心位置の床投影点はおおむね同じ位置にあるとみなしてもよい。

6.FM (Frequency Multiplier,頻度乗数)
頻度乗数FMは、持ち上げ頻度F (Lifting Frequency. 単位: 回/分)、作業時間LD(Lifting Duration)、垂直位置V (Vertical Location. VMで解説済み)から次表を用いて決定する。
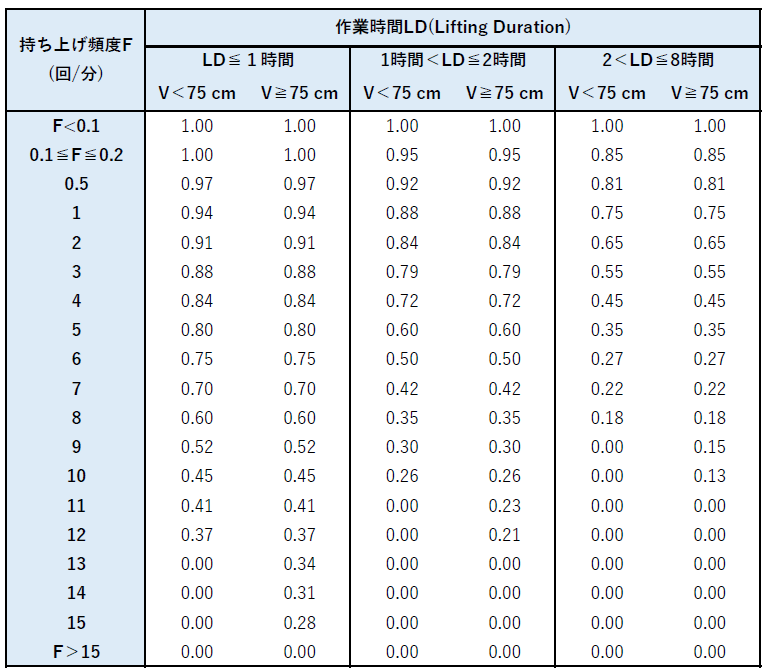
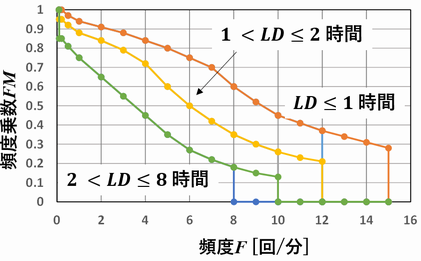
持ち上げ頻度Fが0.2回/分に満たない場合はFは0.2回/分とする。ただしFが更に小さく0.1回/分に満たない場合は十分長い休憩時間が挿入されているとみなし、作業時間LDが1時間以下の分類(LD≦1時間)の頻度乗数FM(つまりFM=1.00)を常に用いる(文献[2]のFMの表に対して、この点は追記されているので注意)。
持ち上げ頻度Fは少なくとも15分間作業を観察して求めるのが基本であるが、頻度が一定しない場合にはより長い時間の観察で求める必要がある。頻度が全く異なる作業が組合わさっている場合はそれぞれ解析すべきであるが、全体としての平均頻度を用いた解析も有効である。
持ち上げ作業が15分以上続かない場合には次のような特別手順をとる。例えば1セッションが8分間の持ち上げ作業(持ち上げ頻度は10回/分)と7分間の非持ち上げ作業あるいは休憩で繰り返される場合には、15分間の平均の持ち上げ頻度Fは10回/分×8分÷15分=5.33回/分と計算する。同様に、1セッションが1分間の持ち上げ作業(持ち上げ頻度は10回/分)と2分間の非持ち上げ作業でこれが繰り返えされる場合には、15分間では5セッションが実行されることになるので、持ち上げ頻度Fは10回/分×1分×5セッション/分÷15分=3.4回/分と計算される。このような場合の作業時間LDの分類は繰り返されたセッションののべ時間とし、セッション中の持ち上げ作業が短いからといっても1時間未満の分類(LD≦1時間)とはしない。
作業時間LDの分類は、作業時間WT (Work Time. この場合は荷物持ち上げ作業時間)と回復時間RT (Recovery Time. この場合は荷物持ち上げ以外の軽い作業あるいは休憩など)の関係で次のように決める。
1)LD≦1時間:1時間以下の持ち上げ作業時間WTがあり、つづいてWTの1倍以上の回復時間RTがある場合がこれに分類される。例えば、45分間持ち上げ作業をして45分間休憩する場合がこの分類に含まれる。RTが短くてWTの1倍に満たない場合は、持ち上げ作業は継続しているとみなし、よりLDの長い分類にする。例えば、30分間持ち上げ作業をして10分間休憩して更に45分間持ち上げ作業をした場合、RTである休憩の10分間はその前のWTである持ち上げ作業の30分に比べて短いので、持ち上げ作業時間LDは30+45分の75分とみなされる(このLDの計算では、間に入っていた10分間の休憩は含めない)。従って、WTは1時間を越えるのでこの分類には属さないことになる。
2)1時間<LD≦2時間:1時間より長く2時間以下の持ち上げ作業時間WTがあり、つづいてWTの0.3倍以上の回復時間RTがある場合がこれに相当する。例えば、90分間持ち上げ作業をして30分間休憩した場合がこれに分類される。RTが短くてWTの0.3倍に満たない場合は、持ち上げ作業は継続しているとみなし、より長いLDの分類にする。
3)2時間<LD≦8時間:2時間より長く8時間以下の持ち上げ作業の場合である。本基準では、持ち上げ作業が8時間以上持続する場合の基準値は提供されていない。
表に値がない場合は近傍の値から直線補間で求める。
7.CM (Coupling Multiplier, 結合乗数)
荷物の持ちやすさに関する乗数で、持ちやすさ (Coupling Type)と垂直位置V (Vertical Location. VMで定義済み)から次表を用いて決定する。
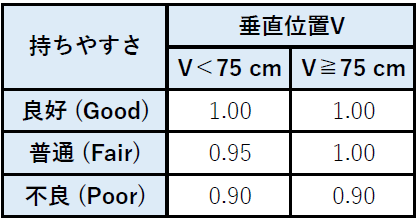
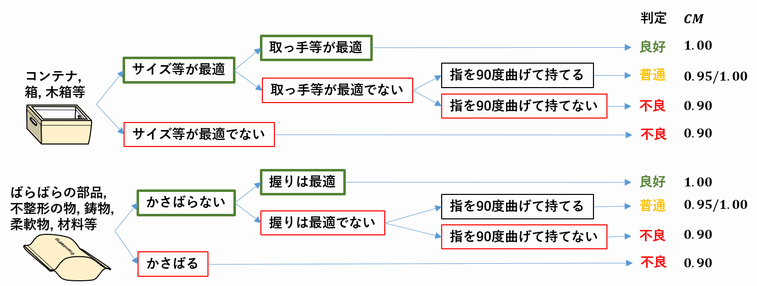
持ちやすさの分類は以下のように決める[2]。
1)良好 (Good):最適に設計されたコンテナ(箱や運搬用木枠など)については、最適に設計された取っ手(ハンドル)や保持用の切り欠き(手掛け穴)があればこれに分類される(注1~3参照)。コンテナに通常入れて運搬しないような原材料などのやわらかい物や不定形の物については、それを手で包み持つことが容易であればこれに分類する(注6参照)。
2)普通 (Fair):最適に設計されたコンテナで、取っ手や保持用切り欠きが最適でなければこれに分類される(注1~4参照)。取っ手や保持用切り欠きのない最適に設計されたコンテナ、やわらかい物や不定形の物については、指を荷物の下に入れてほぼ90度屈曲させて保持できるなら、これに分類される(注4参照)。
3)不良 (Poor):最適に設計されていないコンテナ、やわらかい物、不定形の物などで、かさばる、持ちにくい、角が尖っているなどの場合にこれに分類する(注5参照)。固くなくて持ち上げると真ん中がたわんでしまうような荷物もこれに分類される。
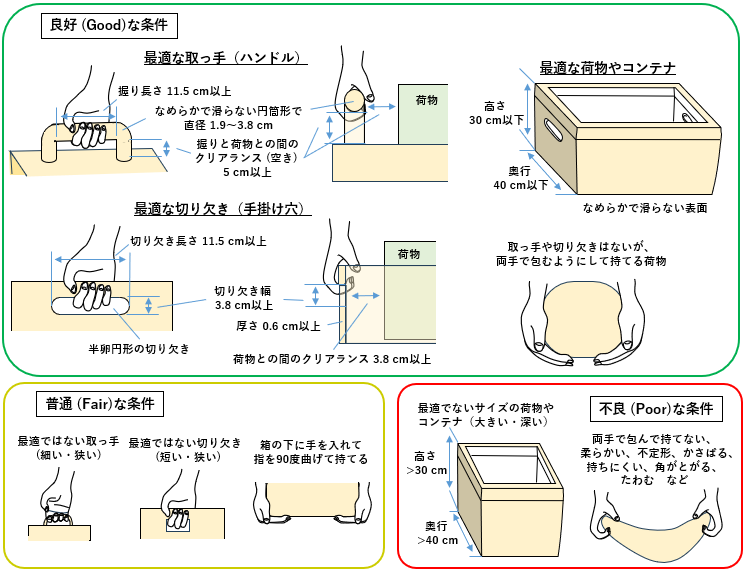
注1)最適に設計された取っ手とは、握りの太さの直径が1.9~3.8 cm、握りの長さが11.5 cm以上、取っ手と荷物の間のクリアランス(隙間)が5 cm以上、握りの形は円筒形で表面はなめらかであるが滑らないというものである。
注2)最適に設計された保持用切り欠き(手掛け穴)とは、切り欠きの幅が3.8 cm以上、長さが11.5 cm以上、半卵円形(semi-oval)、荷物との間のクリアランスが5 cm以上、なめらかであるが滑らず、厚さが0.60 cm以上(つまり、ボール紙の2倍の厚さ)というものである。
注3)最適に設計されたコンテナとは、奥行きが40 cm以下、高さが30 cm以下で、なめらかであるが滑らない表面のものをいう。
注4)床から段ボール箱を持ち上げる場合だと、指を箱の下にいれて約90度屈曲させて持ち上げることができなければならない。
注5)奥行きが40 cmより長い、高さが 30cmより高い、荒いあるいは滑り易い表面、角が尖っている、重心が片寄っている、不安定な内容物、手袋を使う必要があるといった場合、コンテナは最適に設計されているとはいえない。やわらかい物がかさばるというのは、手で持ってバランスがとりにくい場合をいう。
注6)手首が過度に曲がったり、不自然な姿勢になったり、保持するのによけいな力がいるというようなことなく、荷物を保持できなければならない。
原文には図はないが、本サイト管理者が上記の説明に基づいて作成した図を以下に示す(2024-12-02 最適でないサイズの荷物やコンテナを「普通」から「不良」に訂正しました)。
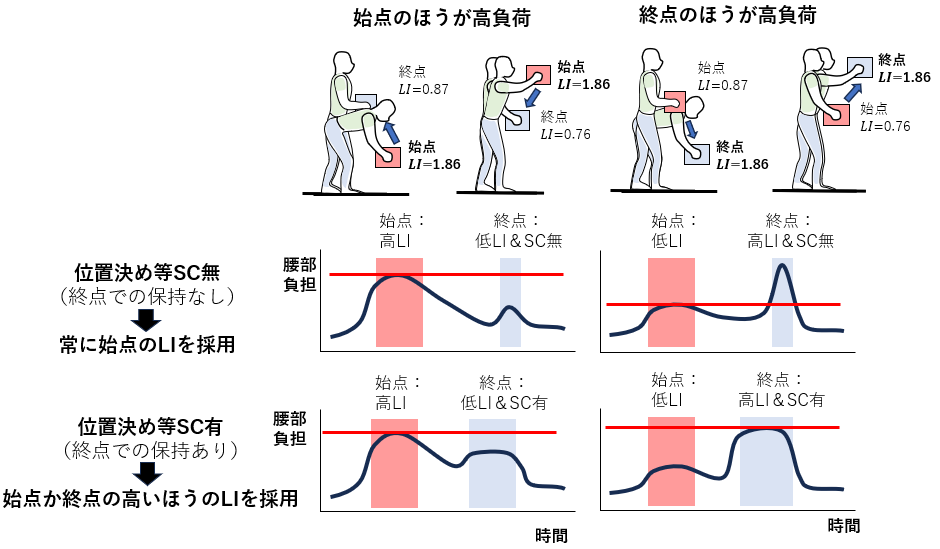
8.終点での位置決め等の特別制御SC:始点と終点のどちらの条件で計算するか
本法は基本的には始点の条件で計算する。ただし、荷物を終点に置くときに次のような位置決め等の特別な制御(Significant Control, SC)が要求される場合には始点と終点の両方のRWL, LIを計算しなければならない。この場合、DM (距離係数)・AM (非対称乗数)・FM (頻度乗数)は始点と同じ値を用いる。始点と終点のRWLをともに求めた場合、作業全体でのRWLとしては、両者のうちの小さいほうの値(つまりより厳しい限界値)を採用する。LIであれば、高いほうの値を採用することになる。
- 終点付近で握り直しをする必要がある場合:始点と終点の垂直位置が大きく異なるために荷物を持ち換える場合や、器具の機械装着のように終点で物を持ち換える必要がある場合がこれに相当する。
- 終点付近で荷物をしばらく保持する必要がある場合:終点に置くタイミングが要求されるため、荷物を持ったままで少し待たされるような場合がこれに相当する。
- 終点に荷物を正確に位置決めして置く必要がある場合:荷物をきれいに積み上げる場合や、機器のガイドにあわせて部品を装着する場合などがこれに相当する。
下図は、終点での位置決め等の特別制御SCの有無による様子を示したものである。位置決め等SCがない場合は、始点での保持開始に時間もかかるので始点でのLIが重要になる。この場合、終点ではごく短時間で荷物を置けるはずなので、終点でのLIは無視される。しかし終点で位置決め等SCがある場合は、終点での保持時間が伸びることになるので、終点でのLIが無視できなくなる。始点より終点のLIが高ければ、終点のLIを選択することになる。(2025-12-07追記)
9.作業中に作業条件が変わる場合の取り扱い
積み上げて置いてある荷物を降ろす作業では、最初は荷物が高い位置にあるので垂直位置Vは高いが、荷物を降ろす作業が進むと次第に垂直位置Vは低くなってしまう。このような場合は、他の係数も考慮して最も厳しい条件(通常はVが最低か最高のところ)の値を採用する。
【4】NLEの複数タスク解析(複合持ち上げ指数CLI)
複数の持ち上げタスクを合わせて解析し、作業全体の強度を示すLIに相当する指数を求めて評価する方法がCLI (Composite Lifting Index, 複合持ち上げ指数)である。CLIを求める方法としては、各タスクについて求めたLIを単純に平均したり頻度乗数FMで重み付けして平均するというやり方が考えられる。この方法は簡単であるが、タスク中で最大のLIよりも常に低いCLIが求められてしまう。つまり、短時間であれ高いLIのタスクがあれば腰痛発症リスクは高くなるという危険性を過小評価することになる。そこでNLEでは、このような問題が生じないように次の仮説を設定している。
- 複数のタスクを行えば、身体負荷あるいは代謝負荷は増大するので常にLIは増大すべきである。
- 複数タスクを実施することによるLIの増え方は、追加して実施されたタスクの性質に依存する。
- 複数タスクを実施することによるLIの増え方は、前に実施したタスクのLIには依存しない。
前述の仮説に基づいたCLIは以下の式で計算される。
CLI = STLI1 + ΣΔLIi
ただし、
STLIi (Single-Task LI): 第iタスクの持ち上げ指数LI.ただし、タスク番号iは、STLIiの値の大きい順につけた番号(つまり、STLI1はSTLIiの最大のもの).
STLIi = Lavi / STRWLi
Lavi (average load weight) : 第iタスクの平均荷物質量Lav. 単位: kg.
STRWLi (Single-Task RWL) : 第iタスクの推奨質量上限RWL.単位kg.
STRWLi = LC×HMi×VMi×DMi×AMi×CMi×FMi
ΔLIi : 第iタスクが加わることにより増加するLIの量.次式で求める.
ΔLIi = FILIi×{ 1/FM(1+2+・・・+i) – 1/FM(1+2+・・・・+i-1) }
ただし、
FILIi (Frequency-Independent LI) : 第iタスクの頻度Fiに依存しない持ち上げ指数LI.
FILIi = Lmaxi / FIRWLi
Lmaxi (maximum load weight): 第iタスクの最大荷物質量Lmax. 単位kg.
FIRWLi (Frequency-Independent RWL): 第iタスクの頻度Fiに依存しない推奨質量上限RWL.単位:kg.
FIRWLi=LC×HMi×VMi×DMi×AMi×CMi
= STRWLi/FMi
FM(1+2+・・・+i): タスク1~iの頻度Fの総和 (F1+F2 +・・・・+Fi, 累積頻度) に対する頻度乗数FM
CLIの例題については、文献[2]を参照のこと。
【5】その他の複数タスク解析法
NLEの当初の提案手法[1][2]には含まれていなかったが、その後NIOSHのWatersらが開発したその他の複数タスク解析手法として、以下の多種持ち上げ指数VLI(Variable Lifting Index)と連続持ち上げ指数SLI (Sequential Lifting Index)とがある。
1.多種持ち上げ指数VLI(Variable Lifting Index)[3] (2025-02-14追記)
積み上げられた多種類の荷物の仕分けやピッキング作業では、荷物質量や作業条件(水平位置や垂直位置)が多彩に変わる。単純に荷物質量・水平距離・垂直位置の組み合わせごとにタスクを分けてLIを計算するとなると、膨大な組み合わせの数のタスクを計算することになる(たとえば質量が5種類の荷物が積み上げられており、その水平距離が3種類、垂直距離が5種類であるなら、始点だけでも5×3×5=75通りの作業条件の異なるタスクが存在することになる)。これを前述した複合持ち上げ指数CLIの手順で評価値を求めることは手続き上は可能であるが、タスク数が10を超えると累積頻度の差が小さくなって誤差がたまりやすいとされる。そこで荷物質量や作業条件をカテゴリ化しかつタスク数が多い場合は6以下に集約することで、データの収集と持ち上げ指数の計算を簡略化したのが、多種持ち上げ指数VLI (Variable Lifting Index)である [3]。
ISOのVLI[5][6]では荷物質量や作業条件をカテゴリ化するVLIのみが紹介されているが、最新のVLIの解説論文である文献[3]では適用場面を想定して以下の2つの方法が解説されている:
1)現場データによる方法(実作業の詳細な作業データが得られる場合):作業条件をカテゴリ化しないで求めた通常のCLIをそのまま採用する。ただしタスク数が10を超える場合は、FILIの6分位数でタスクを6個に集約して求めるVLIを採用する。
2)業務データによる方法(作業の設計段階あるいは作業が多彩すぎて大まかな作業条件のデータしか得られない場合):作業条件のうち水平位置・垂直位置・非対称角はカテゴリ化した値で記録し、同じカテゴリになるタスクを集約してまとめて求めるVLIを採用する。ただし作業条件をカテゴリ化して集約してもタスク数が6個より多い場合は、FILIの6分位数でさらにタスクを6個に再集約して求めたVLIを採用する。
上記の2における荷物質量と作業条件のカテゴリ化と乗数の取扱いは、以下の方法で行う:
(1) 荷物質量Ld:荷物質量が5種類以下ならそのままの値を使用する。5種類を超える場合は、(最大質量-最小質量)÷5の幅で5区分し、各区分に含まれる荷物質量を同一のカテゴリとしてまとめる(最大質量は最後の区分に含める)。各区分の荷物質量Ldは、元タスクの頻度で重みづけした平均質量とする。
(2) 水平位置H:25~40 cmを「近」、41~50 cmを「中」、51~63 cmを「遠」とした3区分とする。各条件での乗数HMの値は、近は0.71 (H=35 cmのHM)、中は0.56 (H=45 cmのHM)、遠は0.40 (H=63 cmのHM)とする。
(3) 垂直位置V:51~125cmを「理想」、それ以外を「非理想」と2区分にする。各条件での乗数VMの値は、理想が1、非理想が0.78 (V=0 cmのVM) とする。
(4) 非対称角A:そのタスクに45度以上の非対称角の割合が50%を超える場合は非対称性ありで乗数AM=0.81 (A=60度のAM)、そうでない場合は非対称性なしでAM=1とする。
(5) 距離乗数DM:始点・終点の垂直位置の差によらず、乗数DMは常に1とする。
(6) 結合乗数CM:経験的に理想的な持ちやすさの状態はまれであることから、常にCM=0.9 (不良)とする。
以上のカテゴリ化で同じ荷物質量・水平位置・垂直位置に分類されたタスクは、1つのタスクとみなして集約する。
集約されたタスクの頻度Fは、同一カテゴリに含まれる元のタスクの頻度の合計値とする。集約された頻度Fから頻度乗数FMを求める際には、垂直位置Vは75 cm未満のほうのFMを用いる。非対称乗数AMのほうも、同一カテゴリに含まれる元のタスクを合わせた非対称性ありの割合が50%を超えるなら非対称性ありでAM=0.81、そうでないなら非対称なしでAM=1とする。
以上の集約したタスクでのLd, HM, VM, AM, DM, FM, CMを用い、集約したタスクのSTRWLi, STLIi, FILIiを改めて求める:
STRWLi = LC×HMi×VMi×DMi×AMi×CMi×FMi
STLIi = Ldi / STRWLi
Ldi : 集約した第iタスクの平均荷物質量. 単位: kg.
FILIi = Ldi / (LC×HMi×VMi×DMi×AMi×CMi)
集約したタスクが6個以下なら、集約したタスクの乗数やSTLIi, FILIiよりCLIと同じ計算法を使ってVLIを求める。
集約したタスクが6個を超える場合は、集約タスクのFILIをソートして6分位数を求め、6分位数で6区分してタスクを6個に再集約する。再集約したタスクのFILIは、その区分に含まれる集約したタスクのFILIの平均値とする。ただし最大の区分のSTLIおよびFILIは、集約したタスクでの最大のFILIとする。再集約された6個のタスクについて、CLIと同じ計算法を使ってVLIを求める:
VLI = STLI1 + ΣΔLIi
ただし、
STLI1:集約したタスクのSTLIiの最大値.
ΔLIi = FILIi×{ 1/FM(1+2+・・・+i) – 1/FM(1+2+・・・・+i-1) }
ただし、
FILIi : 再集約した第iタスクの平均FILIi(ただし第1タスクのFILI1は集約したタスクの最大のFILIi).
FM(1+2+・・・+i): 再集約したタスク1~iの頻度Fiの総和 (F1+F2 +・・・・+Fi, 累積頻度) に対する頻度乗数FM
荷物質量や作業条件のカテゴリ化をしない場合でタスク数が6以下なら、タスクの集約や再集約が不要なので、上記の手続きで計算したVLIの値はCLIと同じになる。
また、荷物質量や作業条件のカテゴリ化を行う場合でも、カテゴリ化による集約でタスク数が10以下になった場合は再集約は不要なので、再集約したタスクのFILIi やFiの代わりに集約して求めたFILIi やFiを用いてVLIを求める。
VLIの詳細および計算例については文献[3][7][8]を参照いただきたい。
(注1)VLIは開発の過程でいくつかの計算法が提案されているが[8]、ここでは最新のVLI紹介論文である文献[3]に従った。
(注2)分位数での区分の取り方は複数あるが、本法のFILIの6分位数は文献[3], [5], [6]の例題では、第1区分の下限値は最小のFILI値、第6区分の上限値は最大のFILI値にして、その間を100/6パーセンタイルずつ6区分する方法が使われている。
(注3)文献[3], [5], [6]には、ISOで追加された片手乗数OM、人数乗数PM、長時間乗数EMの取扱いが明記されていない。文献[7]の妥当性の検証をした論文では、片手乗数OMと人数乗数PMが使用されている。
(注4)終点での位置決め等の制御SCについては、文献[3], [5], [6]の例題ではすべてのタスクのSCが有りのもののみが示されている。ただし手法の定義には、SC有りに限定するとの記載はない。もし、常にSC有りにしてしまうと、カテゴリ化するVLIでは、終点での水平距離が遠くて垂直位置が理想でない場合にはSTLIは最低で一定の値になるので、始点側のバリエーションや改善の効果がVLIに全く反映されないことになる。
(注5)カテゴリ化するVLIでは、最良の条件でも水平乗数HMは0.71、結合乗数CMは0.9とするので、他の条件が最良でもSTRWLは最高でもLCの0.639倍で、LC=23 kgならSTRWL=14.7 kgになる。また、水平距離が51 cm以上かつ垂直位置も理想でないなら、最悪の条件でのHM (0.4) とVM (0.78) が採用されるようになっている。この場合のSTRWLは0.312×LC=7.2 kgとなる。そのため、同じ作業データが得られる場面で、作業条件データをそのまま使って求めたCLIと作業条件をカテゴリ化して求めたVLIとを比較すると、多くの場合はVLIのほうが高めになると予想される。
2.連続持ち上げ指数SLI (Sequential Lifting Index) [4]
CLIの考え方を拡張し、別な時間帯に順次行う複数のタスクの総合的なLIを求めたのが連続持ち上げ指数SLI (Sequential Lifting Index) である[4]。
SLIは以下の式で求める:
SLI=LI1intr+(LI1max-LI1intr)×K
ただし、
K=Σ(LIimax×FTi)/LI1max
ここで、
LI1intr: 最も高ストレスのタスクの連続作業時間LDを考慮したSTLI(単一タスクのLI)
LI1max: すべてのタスクの全体の作業時間を考慮した最も高ストレスのタスクのSTLI
FTi: タスクiにかかった時間(分)÷480分
(480分は1日の労働時間、つまり60分×8時間のこと)
SLIの例題については、文献[4]を参照のこと。
【6】作業設計や作業改善への利用
1.LIについて
LIは、与えられた作業条件がどの程度腰痛の発症リスクを持っているかを示す総合的な評価指数として利用できる。値としてはできるだけ小さいのが望ましく、1以下にすれば腰痛の発症リスクは抑制できるとされている。
LIは複数の作業の比較にも利用できる。通常、異なった条件の作業の負担度の強弱を比較することは困難であるが、LIを作業ごとに求めて比較すれば作業の負担度あるいは改善の重要度の順位付けも可能となる。
LIは、終点での位置決め等の特別制御(Significant Control)の影響評価にも利用できる。つまり、もし始点より終点のLIが大きい場合は、位置決め等による特別制御が不要なように作業改善ができないかを検討する意義があると判断される。
2.各乗数について
HM, VM, DM, AM, FM, CMの乗数の値を比較することで、通常は困難な作業条件のどこを改善するのが最も有効かといった作業要因の順位付けが可能となる。HM, VM, DM, AM, FM, CMの乗数は全て0~1の範囲を取るが、このうち最も小さい値を取る乗数が最も大きい負担度を持つ要因と判断される。値の小さい乗数から改善を進めていけば効果的である。各乗数を1に近くするような一般的な改善法として次のようなものがある。
1)HM (水平乗数):作業者と荷物の間の距離を短くできるように、障害物を取り除いたり荷物のサイズを小さくする。床付近で荷物を取り扱うことがないようにする(足が邪魔になって作業者と荷物の間の距離が長くなるため)。もしそれが不可能なら、足の間に荷物を入れることができるように工夫すべきである。
2)VM (垂直乗数):移動元や移動先の高さを変える。床付近や肩より高い位置での荷物取扱いは避ける。
3)DM (距離乗数):持ち上げあるいは降ろし距離を短くする。
4)AM (非対称乗数):体をひねらなくてすむように、移動元と移動先の位置を近づける。または、歩いて体全体で向きをかえられるように移動元と移動先の位置を離す。
5)FM (頻度乗数):荷物の持ち上げ回数や作業時間を減らす。休憩時間あるいは荷物持ち上げでない軽い作業を行う時間を増やす。
6)CM (結合乗数):荷物や握り手を最適なものに改善する。
3.複数タスク解析について
CLI, VLI, SLIいずれも、1より大きければある程度の障害を発生させるリスクがあると判断される。
タスク別のLIであるSTLIは、それぞれ1以下であることが望ましい。改善をするには最も大きい値のSTLIを示したタスクから改善を試みる。全てのタスクのSTLIが1以下であってもCLIが1より大きい値の場合も同様に改善をする必要がある。
タスク内での改善については、単一タスクの場合と同様に、最も小さい乗数を与える要因を重点的に改善するといった方法を取ればよい。
【7】NLEの計算例
1.単一タスク解析
1)データ収集 取り扱い物質量(平均質量Lavと最大質量Lmax)、荷物の始点と終点での条件(水平位置Hと垂直位置V)、非対称角A、持ち上げ頻度F、持ちやすさ、作業時間LD、特別制御の有無に関するデータを収集する。
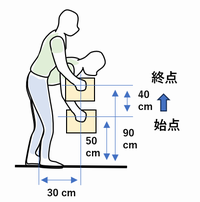
この作業例では下図の作業シーンの図のように、10 kgの荷物を、低い作業台から高い作業台に持ち上げる作業を毎分1回、1時間行う。始点の手の握りの位置は水平距離H30 cm、垂直位置V50 cm、終点は水平距離H30 cm、垂直位置90 cmである。始点・終点とも体のひねりはないので、非対称角Aは0度とする。荷物の持ちやすさは「良好」とする。終点では荷物をきれいに並べておく必要があるので、特別制御(位置決め等)は「あり」とする。
下図では始点と終点の立ち位置は全く同じにしてあるが、1 mまでの足の踏み出しや移動はあってもかまわない。足位置や体の向きが終点で変わる場合は、新に両足内くるぶし中点と移動後の足方向を基準にして水平距離Hや非対称角Aを求める。
| 荷物質量 | 始点 | 終点 | 頻度 F (回/分) | 作業時間LD (時間) | 持ちやすさ | 特別制御 | |||||
| Lav (kg) | Lmax (kg) | H (cm) | V (cm) | A (度) | H (cm) | V (cm) | A (度) | ||||
| 10 | 10 | 30 | 50 | 0 | 30 | 90 | 0 | 1 | 1 | 良好 | あり |
2)各条件の係数計算
式あるいは表から乗数を求める。
| 負荷定数 LC | 水平乗数 HM | 垂直乗数 VM | 距離乗数 DM | 非対称乗数 AM | 頻度乗数 FM | 結合乗数 CM | |
|---|---|---|---|---|---|---|---|
| 始点 | 23 | 0.83 | 0.93 | 0.93 | 1.0 | 0.94 | 1.0 |
| 終点 | 23 | 0.83 | 0.96 | 0.93 | 1.0 | 0.94 | 1.0 |
注1)距離乗数DMは、始点と終点のVの差の絶対値から求める。
注2)特別制御がない場合は、始点のみを計算すればよい。
3)RWLとLIの算出
ここでは特別制御があるので始点と終点でそれぞれRWLを計算する。そして、値の小さいつまり厳しいほうのRWL(ここでは始点)を採用してLIを計算する。
| RWL (=LCxHMxVMxDMxAMxCM) | LI (=Lav/RWL) | |
|---|---|---|
| 始点 | 23×0.83×0.93×0.93×1.0×0.94×1.0=15.5 | 10/15.5=0.65 |
| 終点 | 23×0.83×0.96×0.93×1.0×0.94×1.0=16.0 | - |
4)解釈
ここではLIは0.65と1より小さいので、この作業条件による筋骨格系障害のリスクは低いと判断される。
さらにリスクを軽減するには、まず最も小さい値を示した係数の改善を検討する。ここでは水平乗数HMが0.83と最も小さいので、水平距離H(荷物と体の距離)を小さくするように改善する(もっとも、ここではすでに水平距離Hはそれほど大きくないので得られる改善度も小さい)。
2.複合タスク解析(複合持ち上げ指数CLIの例)
1)データ収集
各タスクについて、単一タスクの場合と同様に水平位置H、垂直位置V、垂直移動距離D、非対称角A、持ち上げ頻度F、持ちやすさ、作業時間LDに関するデータを収集する。
この作業では、3種類のタスクを同じ1時間の作業時間内に行う。タスク1は10 kg、タスク2は20 kg、タスク3は15 kgの荷物をそれぞれ持ち上げる作業である。3つのタスクの作業時間LDは同じ値にする(頻度や順序のために厳密には多少の違いはあるかもしれないが、それは無視する)。
| タスク | 荷物質量 | 始点 | 終点 | 頻度 F (回/分) | 作業時間LD (時間) | 持ちやすさ | 特別制御 | |||||
| Lav (kg) | Lmax (kg) | H (cm) | V (cm) | A (度) | H (cm) | V (cm) | A (度) | |||||
| 1 | 10 | 10 | 30 | 50 | 0 | 30 | 90 | 0 | 1 | 1 | 良好 | あり |
| 2 | 20 | 20 | 40 | 20 | 0 | 40 | 90 | 0 | 2 | 1 | 良好 | あり |
| 3 | 15 | 15 | 30 | 40 | 0 | 30 | 80 | 0 | 1 | 1 | 良好 | あり |
2)各条件の乗数計算
単一タスク解析の時と同様に、式や表などから乗数を求める。
| タスク | LC | HM | VM | DM | AM | FM | CM | |
|---|---|---|---|---|---|---|---|---|
| 1 | 始点 | 23 | 0.83 | 0.93 | 0.93 | 1.0 | 0.94 | 1.0 |
| 終点 | 23 | 0.83 | 0.96 | 0.93 | 1.0 | 0.94 | 1.0 | |
| 2 | 始点 | 23 | 0.63 | 0.84 | 0.88 | 1.0 | 0.91 | 1.0 |
| 終点 | 23 | 0.63 | 0.96 | 0.88 | 1.0 | 0.91 | 1.0 | |
| 3 | 始点 | 23 | 0.83 | 0.90 | 0.93 | 1.0 | 0.94 | 1.0 |
| 終点 | 23 | 0.83 | 0.99 | 0.93 | 1.0 | 0.94 | 1.0 | |
注1)距離乗数DMは、始点と終点のVの差の絶対値から求める。
注2)特別制御がない場合は、始点のみを計算すればよい。
3)STLIやFILIの計算
STLIとFILIを求めるとともに、STLIの大きい順に新タスク番号を決める。STLIに同値のものが複数あった場合、繰り返し頻度Fが大きい方に小さい番号をつける。特別制御がある場合は、始点と終点のSTLIのうち大きいSTLIを与えるほうのみをそのタスクのデータとして用いる(ここでは*をつけたほうがそれに相当する)。
| タスク | FIRWL (=LCxHM xVMxDM xAMxCM) | FILI (=Lmax /FIRWL) | STRWL (=FIRWLxFM) | STLI (=Lav/STRWL) | 新タスク 番号 | |
|---|---|---|---|---|---|---|
| 1 | 始点 | 16.5 | 0.61 | 15.5 | 0.64* | 3 |
| 1 | 終点 | 17.0 | 0.59 | 16.0 | 0.62 | ・ |
| 2 | 始点 | 10.7 | 1.87 | 9.7 | 2.05* | 1 |
| 2 | 終点 | 12.2 | 1.63 | 11.1 | 1.80 | ・ |
| 3 | 始点 | 16.0 | 0.94 | 15.0 | 1.00* | 2 |
| 3 | 終点 | 17.6 | 0.85 | 16.5 | 0.91 | ・ |
4)複合持ち上げ指数CLIの計算
★以下の計算では新タスク番号を使用する。
この例ではタスクが3つなので
CLI = STLI1 + ΔLI2 + ΔLI3
= STLI1 + FILI2 x {1/FM(1+2) – 1/FM(1)} + FILI3 x {1/FM(1+2+3) – 1/FM(1+2)}
ここで、 FM(1): F1=2, V1=20, LD1=1 なので表よりFM(1)=0.91.
FM(1+2): 新タスク番号1と2のFの和=2+1=3, V2=40, LD2=1なので 表よりFM(1+2)=0.88.
FM(1+2+3): 新タスク番号1,2,3のFの和=2+1+1=4, V3=50, LD3=1 なので、表よりFM(1+2+3)=0.84.
従って、
CLI = STLI1 + FILI2 x {1/FM(1+2) – 1/FM(1)} + FILI3 x {1/FM(1+2+3) – 1/FM(1+2)}
= 2.05 + 0.94 x(1/0.88-1/0.91) + 0.61x(1/0.84-1/0.88)
= 2.12
注1)FM(1+2+・・・+i)を求めるときにFの総和に小数部がある場合は、FMの表中の近傍の値から直線補間でFMの値を求めること。
注2)FM(1+2+・・・+i)を求めるときに、Fの総和が大きすぎる(作業時間LDが2時間超で手位置V1が75 cm未満だと8回/分が上限)とFM(1+2+・・・+i)が0になり、CLIは計算できなくなる。
注3)高負荷だがFが0.1回/分より小さいタスクが複数あると、Fの総和に応じたFM(1+2+・・・+i)に差が出なくてΔLIiが0になり、その影響がCLIに反映されない場合がある。
5)解釈
CLIは2.12と1より大きいので、ある程度の障害を発生させるリスクがあると判断される。その場合の優先順位としてはSTLIの最も大きいものから対応すべきなので、ここではタスク2が問題になる。タスク2については、最も値の小さい乗数は水平乗数HMなので、水平距離を短くするように改善することが必要である。具体的には、たとえば荷物のサイズが大きいとか荷物を置く場所に十分近づけないような障害があるならそれを改善することになる。
【8】ISO 11228-1 (JIS Z8505-1) の持ち上げ
ISO 11228-1 (JIS Z8505-1) の持ち上げは、NLEを拡張したものである。
NLEのRWLは、ISOではRML(Recommended Mass Limit) と呼ぶ。LIは同じである。RMLおよびLIを求める式は以下のとおりである:
RML=mref×hM×vM×dM×αM×fM×cM×oM×pM×eM
LI=m/RML
ここで、mrefは参照質量(reference mass)でNLEの負荷定数LCに相当する値、mは荷物質量でNLEのLavに相当する値である。ISOにはNLEのLmaxはなく、Lmaxの代わりにmを用いる。
NLEのLCは23 kgで一定の値であったが、ISOのmrefは対象集団によって値を選択することができる。男女合わせた一般労働者集団についてはNLEと同じmref=23 kgまたは25 kgを使用する。男女別の対象集団については、年齢層も考慮して以下の値が利用できる:
・女性・20~45歳:mref=20 kg
・女性・20歳未満または45歳以上:mref=15 kg
・男性・20~45歳:mref=25 kg
・男性・20歳未満または45歳以上:mref=20 kg
乗数については、ISOのhM, vM, dM, αM, fM, cMは、それぞれNLEのHM, VM, DM, AM, FM, CMに相当し、計算法も同じである。ISOで追加された乗数は以下のとおりである:
1)片手乗数oM:作業を片手で行うなら0.6、両手なら1とする。なお、片手作業の場合の非対称角α(NLEのA)は、荷物を持ったほうの手の握りの床投影点を非対称面方向とみなして角度を求める(荷物重心位置の床投影点と荷物を持った手の握りの位置の床投影点がおおむね一致するため)。
2)人数乗数pM:作業を1人で行うなら1,2人または3人で行うなら0.85とする。この場合、荷物質量mと推奨質量上限RMLは、人数で割った値で計算する。
3)長時間乗数eM:1日の労働時間が8時間以上の場合に使用する。8時間以下は1,8時間超9時間以下は0.97、9時間超10時間以下は0.93、10時間超11時間以下は0.89、11時間超12時間以下は0.85とする。
複数タスク解析については、ISOにはNLEの複合持ち上げ指数CLIのほか、前述した多種持ち上げ指数VLI (Variable Lifting Index)と 連続持ち上げ指数SLIも含まれている。
【9】持ち上げ指数LIの解釈の再検討
NLEが公表されたのち、LI、CLI、VLIおよびISOの持ち上げの利用が広がり、多くの疫学調査に基づいて、LIの判定基準の妥当性が再検討された [5][6][7]。その結果、LIは以下のように判定・評価するようになった。リスクを低・中・高の3段階で判定するなら、LI≦1.5であれば低リスク、1.5<LI≦2.0なら中リスク、LI>2.0なら高リスクとする。
- LI≦1.0:リスクは非常に低い。健常な対象集団であれば措置は不要
- 1.0<LI≦1.5:リスクは低い。低頻度・高負荷条件や極端な姿勢または静的姿勢に特に注意し、必要に応じて追加の分析を行う。
- 1.5<LI≦2.0:リスクは中程度。LIを低減するために優先順位に応じた作業・作業場の見直しを行い、効果検証のために結果を分析する。
- 2.0<LI≦3.0:リスクは高。LIを低減するため、作業の変更を優先度高く実行することが望ましい。
- LI>3.0:リスクは非常に高。LIを低減するため、作業の変更を即座に実行することが望ましい。
【10】適用範囲
NLEおよびISOの持ち上げは、次のような荷物取り扱いには適用できない。
- 片手での作業 (ISOは対応可)
- 複数人での作業 (ISOは3人まで対応可)
- 8時間以上の作業 (ISOは12時間まで対応可)
- 座った姿勢あるいはひざまずいた姿勢での作業
- 作業空間が制約されている場合
- バランスのとれない荷物の取扱い
- 運搬や押したり引いたりするような作業での荷物取扱い
- 手押車やショベルを使用する作業にともなう荷物取扱い
- 速い速度での荷物取扱い(おおよそ75 cm/秒を越えるもの)
- 足元が悪い場合(靴と地面との間の摩擦係数が0.4未満の場合)
- 温熱環境が悪い場合(温度19~26℃、湿度35~50%の範囲にない場合)
【11】適用場面の例
作業場面でよくみられる作業条件による負担の影響を、各乗数の変化とそれによる推奨質量上限RWLの増減で以下に示す。図中の「○○%増」は、(改善後乗数÷改善前乗数-1)×100 [%]で求めた値である。
1)水平距離H
水平乗数HMは最低が0.40と、他の乗数に比べて低下が大きく、RWLへの影響が大きい。
(1)棚の前に物をおかない
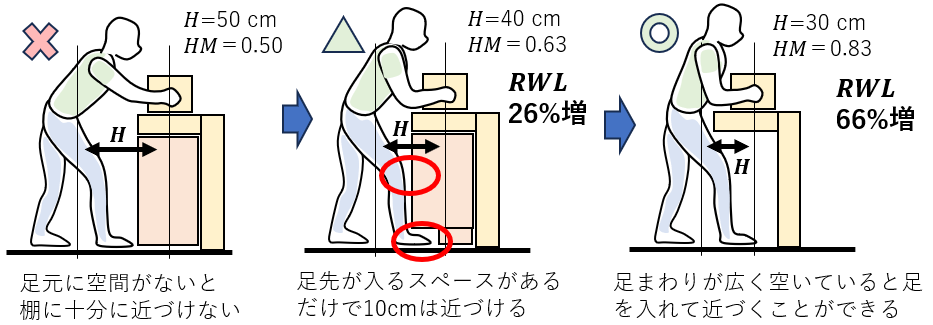
足元に荷物が置かれていると、足先や膝が荷物にあたるので、棚に十分に近づけない。
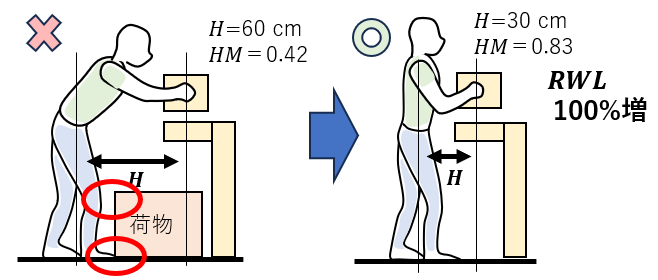
棚の前に置かれた荷物が小さくて足元にあるだけでも、意外に影響が大きい。
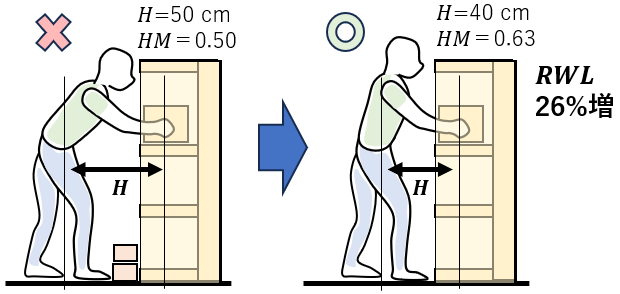
(2)足まわりの空間を適切に確保する
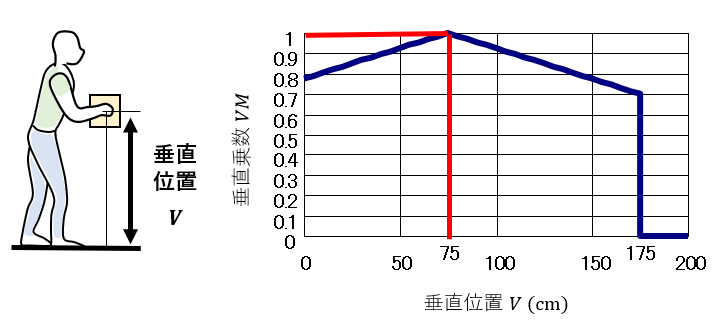
2)垂直位置V
垂直乗数VMは、ナックル高である75 cmが1で、その前後で低下する。
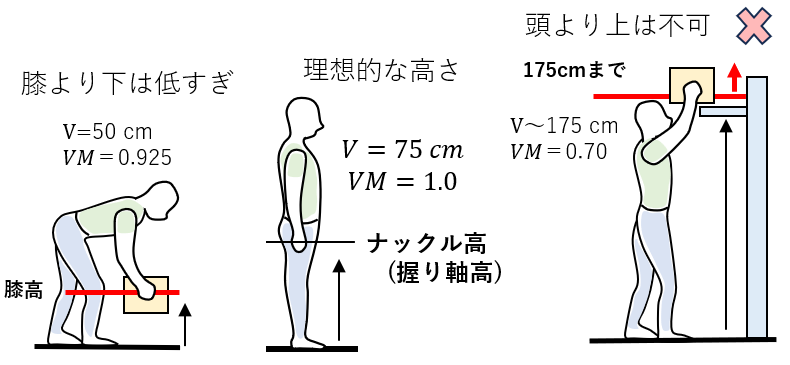
(1)荷物の質量と望ましい垂直位置
高いところや低いところは垂直乗数VMが小さくなるので、重い荷物を置くのは避けてほしい。
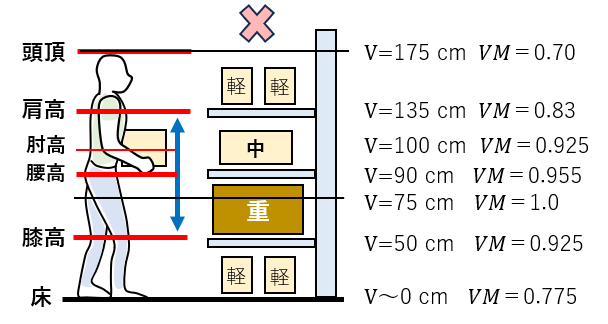
(2)腰高付近に下げると有利
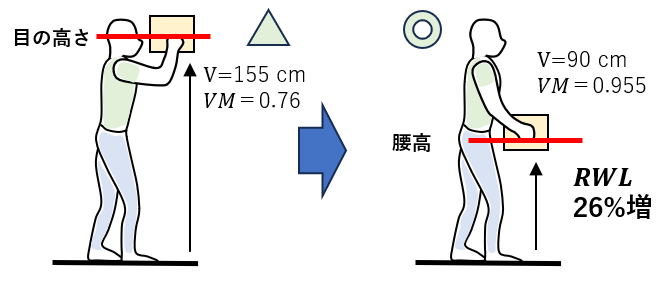
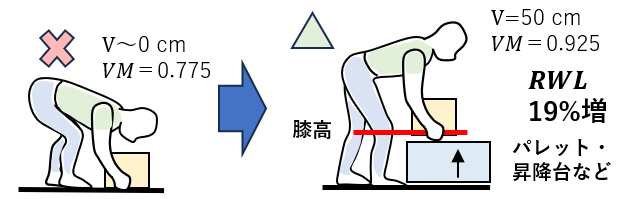
(3)床面からの持ち上げは避けたい
床面から持ち上げなくて済むようなパレットや昇降台などがあるとよい。
荷物やコンテナの高い位置に持ち手がついていると、それだけでも25 cmくらいはVが高くなり、VM=0.85となってRWLは10%増になる。
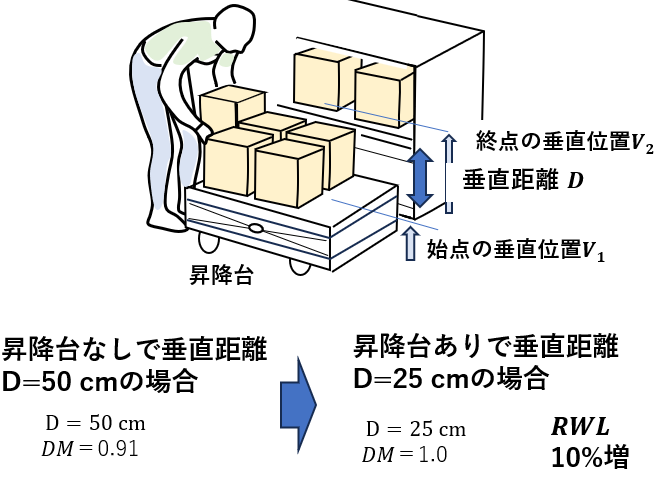
3)垂直距離D
距離乗数DMは最低が0.85と、他の乗数に比べて低下が少ない(VLIで省略された理由)。
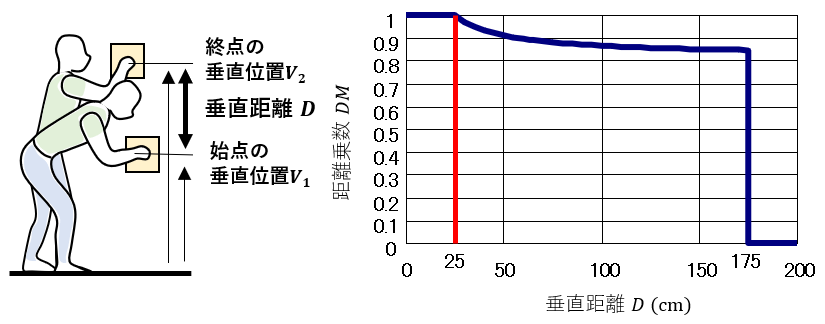
作業台や昇降台などを利用して、始点と終点の高さの差D を25cm以下にできると、距離乗数DM=1.0になって、RWLを高くできる。ただし、改善効果はやや小さめである。
始点と終点を同じ高さにして滑らせて運べる場合には、持ち上げではなく、押し引き作業になるので、腰への負担が大きく低減できる。
4)非対称角A
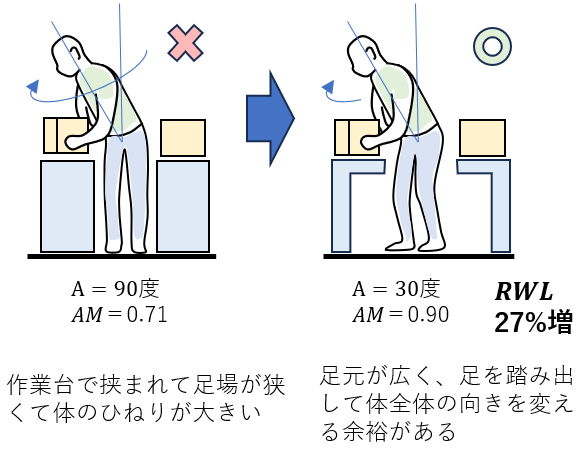
非対称乗数AMは最低が0.568と、他の乗数に比べて変化は大きい。しかし多くの場合は、90度を超える非対称角での作業は一般的でなく、かつ、足が動いて持ち上げ方向に向いたり反対側の足が浮いたりして体の向きが変わるので、そこまでは大きく変化しない。
ただし足回りに物があるなどしてスペースがないと、足や体が動かせず、レイアウト通りの非対称角で作業することになる。
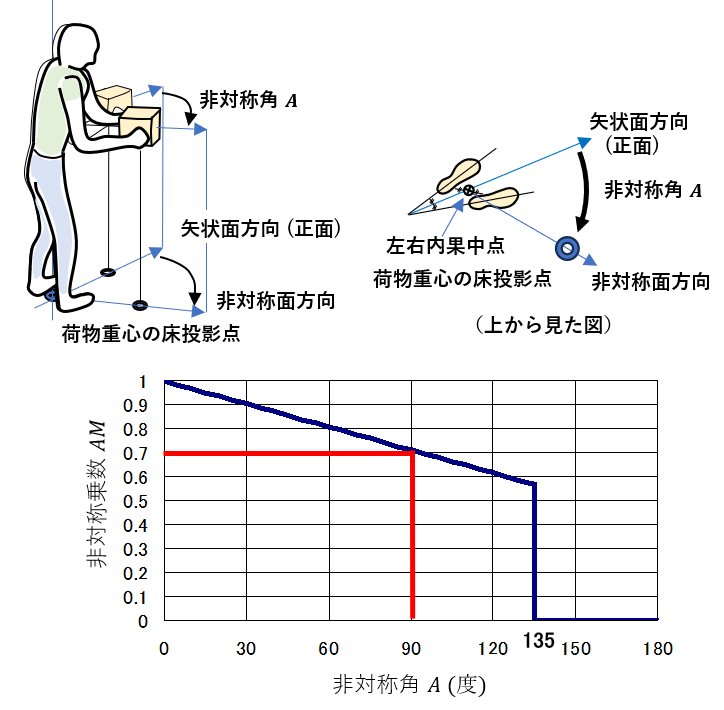
体のひねりを伴う非対称作業では、足まわりの空間を確保して、足の踏み出しや体の向きの変更が可能なようにする。
5)荷物サイズ
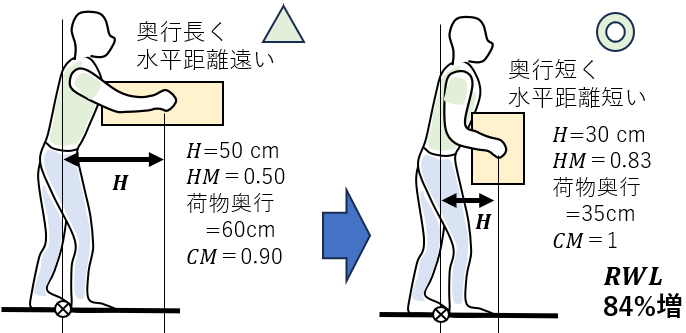
腰痛予防の点では、荷物のサイズのうち、左右の幅よりも前後の奥行を狭くするほうが優先される。これは水平距離Hに影響するためである。
そのため、荷物やコンテナの奥行(前後方向)はできるだけ短くし、大きすぎるコンテナは使わないこと。
荷物が大きすぎて適切に保持できなくなると、持ちやすさが不良で結合乗数CM=0.90となり、 RWLは10%減る。
水平距離 Hが50 cmから30cmになると、水平乗数HMが0.50から0.83になり、RWLは約1.7倍になる。荷物の奥行きが40cmを超えているなら、結合乗数CMも0.9となる。こちらも改善されるなら、RWLは84%増(=(0.83×1)/(0.5×0.9)-1)になる。
6)作業人数P (ISO)
大きな荷物を1人で持つと、水平距離Hが長くなり、水平乗数HMが小さくてリスクが高くなる。
2人作業にすると1人分の荷重がLd/2 [kg]になり、水平距離Hも短くなる(荷物による力の作用点が重心位置から手の保持位置に変わるため)。ただし人数乗数PM=0.76がかかる。そのため、下図の例ではRWLは、2人分なら2.52倍、1人あたりなら1.26倍(26%増)になる。
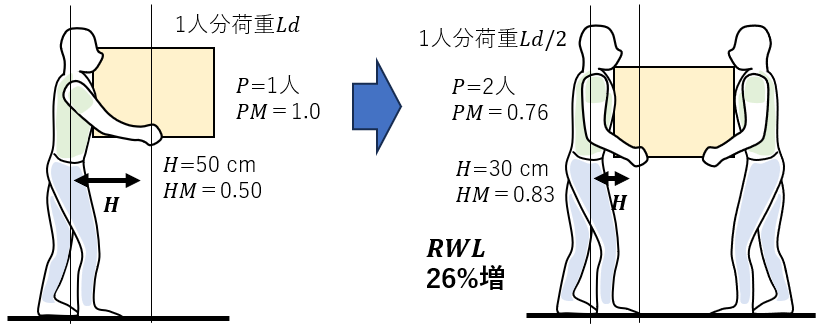
重いが小さな荷物だと、1人でも2人で水平距離はあまり変わらない。その場合、2人作業のRWLは、人数乗数PM=0.76 があるので、2人分ならRWLは1.52倍(52%増)だが、1人あたりなら0.76倍(24%減)に留まる。
同様に3人作業で水平距離がほぼ変わらなければ、人数乗数PM=0.5なので、RWLは3人分なら1.5倍(50%増)だが、1人あたりなら0.5倍(50%減)に留まる。
多人数作業での乗数PMが2人あるいは3人で1より小さくなるのは、複数人になると協調動作が必要であり、身長の違いや荷物の重心位置のずれなどで必ずしも1人のRWL×人数が得られないことを示している。
7)終点での位置決め等による特別制御SC (2025-12-07追記)
本法では、終点で位置決め等がない(SCが無)の場合は始点のLIを採用し、SCがある場合は始点と終点のLIの大きいほうを採用する。従って、SCの有無により、始点と終点のいずれの作業条件を改善すべきかを変える必要がある。下図はその様子を示したものである。
終点で位置決め等SCがない場合は、シンプルに始点のLIを低減するように作業を改善する。
終点で位置決め等SCがある場合は、始点か終点の高いほうのLIの位置での作業を改善する。ただし終点のLIが高い場合は、終点でのLIを下げる改善のほか、位置決めをなくすという改善法もある。位置決めをなくす方法としては、整列させずに置けるように工夫する(整列はコンベヤやガイドを利用する)、終点で精密な位置合わせをして組付けたりはめ込んだりする作業をなくすといった方法があるだろう。

参考文献
- Waters TR, Putz-Anderson V, Garg A, Fine LJ. Revised NIOSH lifting equation for design and evaluation of manual lifting tasks. Ergonomics 1993,36(7),749-776.
- Waters, TR., Putz-Anderson, V., Garg, A., “Applications manual for the revised NIOSH lifting equation”, DHHS (NIOSH) Publication No. 94-110 (Revised 9/2021), DOI: https://doi.org/10.26616/NIOSHPUB94110revised092021
- Waters, T., Occhipinti, E., Colombini, D., Alvarez-Casada, E., Fox, R.., Variable lifting index (VLI): A new method for evaluating variable lifting tasks. Human Factors, 2016, 58(5), 695-711. DOI: 10.1177/0018720815612256
- Waters, TR., Lu, M.L., Occhipinti, E., New procedure for assessing sequential manual lifting jobs using the revised NIOSH lifting equation. Ergonomics 2007, 50(11), 1761-1770.
- ISO, ISO 11228-1:2021 Ergonomics – Manual handling – Part 1: Lifting, lowering and carrying.
- JIS Z8505-1:2025, 人間工学-手作業による取扱い-第1部:持ち上げ,持ち下げ及び運搬, 日本規格協会, 2025.1.20
- Battevi, N., Pandolfi, M., Cortinovis, I., Variable lifting index for manual-lifting risk assessment: A preliminary validation study. Human Factors 2016, 58(5), 712–725. DOI: 10.1177/0018720816637538
- Colombini, D., Occhipinti, E., Alvarez-Casado, A., Waters, TR., “Manual Lifting – A Guide to the Study of Simple and Complex Lifting Tasks”, CRC Press, 2012, ISBN 9781439856635
(補足説明1)なぜ、NLEには作業姿勢の要因が含まれていないのか
作業姿勢や動作の改善活動を人の姿勢をベースに進めてきた人にとって、NLEに姿勢の要因が入っていない点は不思議に感じる。たとえば、どういう姿勢で持ち上げをするのか指定できればRWLをより正確に推定できそうだし、実際の持ち上げの姿勢が不適切ならその影響をRWLで示すことで作業改善に利用できるのではないかと思うだろう。
本法に作業姿勢の変数が含まれていないのは、本法が人の姿勢や動作を直接制限するような管理的な改善を目指しておらず、あくまで作業する場や荷物といった人以外の作業場の設計による改善(工学的な改善)に焦点を絞っているためである[1]。人の姿勢や動作を直接管理する方法は、その導入も維持も難しい。しかし人の姿勢や動作は、作業環境(作業面の距離や高さ、設備の配置など)で決まることが多い。そのため、作業環境を適切に設計する工学的な改善をするほうが間接的であっても効果は現れやすい[1][2]。
NLEの初版 (1981年版NLE)であるWork Place Guide for Manual Lifting [2]によると、NLEの構築の過程で研究者らは疫学・生体力学・生理学・心理物理学の4つの分野および管理的改善(人の選別と訓練)と工学的改善(作業条件の改善)の2つのハザード管理の観点から、NLEの構築を進めた。その結果として選ばれたのが、荷物質量、荷物の水平距離、垂直位置、持ち上げ距離、持ち上げ頻度、作業時間という作業要因の変数である。管理的な面に相当する人の選別は、選別のための検査が医学・コスト・法令の観点で当時は未熟であるとして採用していない。同様に不良姿勢を避けるようにといった教育・訓練についても、当時は十分なエビデンスがなかったこともあって考慮していない。
改訂版のNLE(RNLEあるいは1993年版NLE)[3]においても同様な観点で検討し、乗数への変換法の見直し、非対称性等の変数の追加、複数作業への対応(CLI)を行っている。作業姿勢に関しては、頻度乗数の改定で想定した持ち上げ方はStoop法(足が伸びたままで体幹を前傾させて腰背部の筋で持ち上げる方法. back lift)であり、これはSquat法(体幹の前傾を抑えて足の屈伸で持ち上げる方法. leg lift)だとエネルギー消費が高すぎて高頻度の反復持ち上げを遂行できないためと記述されている。一般に持ち上げ方法としてはStoop法よりもSquat法のほうが望ましいと言われることが多いが、本法を検討した研究者らはそのように判断していない。確かに小さくて重い荷物を体の近くで扱うなら、Squat法のほうが腰部への負荷は小さくなる(よく見かけるSquat法のイラストで荷物を両足の間に入れているのはこのため)。しかし荷物が大きいと、Squat法では膝が邪魔になるので、体の前傾が強くなって腰部負担は高くなる。このことは初版のNLE[1]でも触れられている。それ以外にも、動的持ち上げだと両者の差があまりないこと、スクワットが余裕で反復できる脚力を持った人はそもそもあまりいないこと、作業姿勢の訓練がいまひとつ効果が上がらないことなどがある。これらを踏まえ、少なくとも本法が対象とする反復の持ち上げ評価においては、初版・改訂版を通して直接的に姿勢や動作を考慮する意義を認めなかったようである。
以上のように、NLEは初版から工学的管理を優先した評価法であり、作業姿勢に対する直接的な評価は含んでいない。一般に職場のハザードコントロールにおいては、本質的あるいは工学的改善が効果的で、管理的改善あるいは個人保護具は効果が低いとされる。ただし、全体の改善効果と満足度を高めるには、工学的改善だけでなく管理的改善も含めて総合的にアプローチするほうがよいのも事実である[4][5]。NLEの観点での介入はIE(インダストリアルエンジニアリング)や生産技術の関係者にとっては受け入れやすく、管理的改善は産業保健関係者にとって受け入れやすい。全身の作業姿勢そのものを直接評価する方法としてはOWASやREBAがあり、必要に応じてこれらを併用するとよい。
[1] Stephan Konz, NIOSH lifting guidelines, American Industrial Hygiene Association Journal, 43(12):931-933 (1982)
[2] NIOSH, Work Practices Guide for Manual Lifting, NIOSH Technical Report No.81-122, 1981, U.S. Department of Health and Human Services, Public Health Service. Centers for Disease Control. National Institute for Occupational Safety and Health. Cincinnati, OH. US, https://www.cdc.gov/niosh/docs/81-122/default.html
[3] Waters TR, Putz-Anderson V, Garg A, Fine LJ. Revised NIOSH lifting equation for design and evaluation of manual lifting tasks. Ergonomics 1993,36(7),749-776.
[4] James P. Kohn, “Ergonomics Process Management: A Blueprint for Quality and Compliance”, CRC Press, 1998
[5] Christopher Hamrich, Chapter 13: Engineering controls – What works and what does not, in: Marras, B. & Karwowski, W. eds., The Occupational Ergonomics Handbook (2nd Ed.). Volume 2: Interventions, Controls, and Applications in Occupational Ergonomics. (2nd Ed.). CRC Press, 2006, 13-1-13-14.
(補足説明2)なぜNLEの負荷定数LCは23 kgなのか
NLEは米国で作られたので、LCが23 kgと中途半端なのはポンドからの換算のためかと思った人もいるかもしれないが、LCはポンドでは51 lb [1]なのでもっと中途半端に見える。この理由は以下のとおりである。
NLE (RNLE) の初出の論文[1]の6.2においてLCは、理想的な持ち上げ条件での最大持ち上げ質量に基づいて心理物理量と生体力学の基準により決めたと記されている。ここでの理想的な持ち上げ条件とは、ひねりなし (sagittal position)、頻度はまれ (occasional lifting)、持ちやすさは良好 (good coupling)、持ち上げ距離は25 cm以下などであると記されている。また、理想的な持ち上げ条件では75%の女性労働者および90%の男性労働者が受け入れられることが望ましく、そうすれば腰部椎間板圧縮力も3,400 Nを下回るとしている。
さらに同論文によると、NLEの初版ではLCは40 kgであったのを改訂で23 kgと大きく低下させたように見えるが、これは改定では水平距離の基準が15 cmから25 cmと遠くなったのが主因で、これを補正すると実質的には1kg分ほど軽くしただけであり、この1 kg分軽くしたのはSnook tablesの1978年版[2]の限界値が1991年版[3]で下がったためであると述べている。
以上の記述を基に、1991年版のSnook & Ciriello tablesの値(文献[3])を確認すると、女性の持ち上げの表(Table 3)で、頻度が最低(8時間に1回)、持ち上げ距離が最少 (25 cm)、対象集団が75パーセンタイルの条件で許容限界が23 kgとなるところを探すと、高さが「床からナックル高」で荷物サイズが最少の「34 cm」の条件の組み合わせのみがちょうど23 kgになっていた(Table 5の持ち下げも23 kg)。この2つの条件は、確かにSnook & Ciriello tablesの条件の中では最も高い許容限界質量となっているので、理想的な持ち上げ条件にあたる。また、同じ条件の1978年版のSnook tablesの値(文献[2]のTable 2)の値をみると31 kgとなっており、1991年版のほうが1978年版よりも値は下がっているという文献[1]の記述とも矛盾しない(持ち下げはTable 4より32 kg)。これより、23 kgという値がSnook & Ciriello tablesのある条件の値をそのまま採用した可能性がある。
ただしこれだけだと決め手に欠けるのでさらに文献を探ったところ、Snook自身によるSnook & Ciriello tablesの紹介論文[4]のなかに、NLEのLCについての記述が見つかった。この文献の13.7でSnookは、「NLEのLCが23kgなのは、Snook & Ciriello tables (1991)の女性の75パーセンタイルの持ち上げで、「床からナックル高」の範囲、まれな頻度(8時間に1回)、小さい荷物(幅34 cm)、短い持ち上げ距離 (25 cm)、持ちやすい条件のところの値が23 kgなのを参照したため」と述べている。前述の推定した作業条件の部分も、まったく同じになっている。
以上より、LCが23 kgなのは、Snook & Ciriello tablesのこの条件の値をそのまま採用した、つまり実測実験に基づく値をそのまま採用したからとのことで間違いないなさそうである。
(補足1)文献[1]で、LCは確かにSnook & Ciriello tablesの持ち上げの女性の75パーセンタイルを参照したが、作業条件の乗数を組み合わせた条件(理想的でない持ち上げ条件)ではSnook & Ciriello Tablesの女性の90%までカバーされることも示されている (Table 5)。
(補足2) Snook & Ciriello tablesは、データを追加して今はLM-MMH式に更新されている。そこでLM-MMH式で同じ条件の値を求めてみる。女性・持ち上げ・75%・水平距離H=0.38 m・高さV=0.22 m・上げ下げ高さDV=0.25 m・反復回数F=1/480 回/分とすると、MAL=22.04 kgとなった。新しいデータを追加したLM-MMH式に基づくなら、LCは1 kgほど低い22 kgになる。
(補足3)ISO 11228-1の持ち上げ [5]では、NLEの負荷定数LCに対応する参照質量mrefとして25 kgを基本的に使用するが、23 kgのほか対象集団に応じて15 kg, 20 kg, 25 kgを使用することも可能とされている。操作力のデータは個人差が大きい(変動係数CVが0.3前後)。そのため、サイズ (CVが0.05前後)の設計のように90~95パーセンタイルが受容できるようにすると、現実的な作業設計ができなくなる(多くの作業が許容不可になる)。それも踏まえて操作力に関しては、75~85パーセンタイルの値が許容限界に採用されることが多い。ISOのmrefについては、Annex BのTable B.1に示すように25 kgで男女合わせて85%がカバーされるので、基本的には25 kgを採用し、あとは対象作業者に応じて(あるいは国内の指針等との整合性も踏まえて)ユーザが使い分けるようになっている。
[1] Waters TR, Putz-Anderson V, Garg A, Fine LJ. Revised NIOSH lifting equation for design and evaluation of manual lifting tasks. Ergonomics 1993,36(7),749-776.
[2] Snook, S.H., “The design of manual handling tasks”, Ergonomics, 21, 12, pp.963-985, 1978, doi: 10.1080/00140137808931804.
[3] Snook, S.H. and V.M. Ciriello, “The design of manual handling tasks: revised tables of maximum acceptable weights and forces”, Ergonomics, 34, 9, pp.1197-1213, 1991, doi: 10.1080/00140139108964855.
[4] Stover H. Snook, 13. Psychophysical tables: Lifting, lowering, pushing, pulling, and carrying, in: “Handbook of Human Factors and Ergonomics Methods”, eds., Neville Anthony Stanton, Alan Hedge, Karel Brookhuis, Eduardo Salas, Hal W. Hendrick, CRC Press, August 30, 2004, 13-1-13-23, ISBN 9780415287005
[5] ISO, ISO 11228-1:2021 Ergonomics – Manual handling – Part 1: Lifting, lowering and carrying.