Liberty Mutual のMMH式の概要
【1】概要
Liberty MutualのMMH式(LM-MMH: liberty Mutual manual materials handling equation)[1]は、Liberty MutualのPotvinらが作成した手作業による荷物取り扱いにおける荷物質量の取扱い限界を求める式である。荷物持ち上げ・運搬・押し引きのMMHの代表的な3種類の作業すべてに対応している。LM-MMHは、従来、SnookとCirielloが作成して広く世界で利用されていたSnook & Ciriello Tables [2][3]に新たな実験データを加えて回帰式の形で再整理されたものである。
本家のWebで利用できるLM-MMHは以下のリンクで公開されている。
https://libertymmhtables.libertymutual.com/
【2】Snook & Ciriello Tablesについて
荷物の取扱い作業は、全身の無数の関節の自由度と多数の筋を動員して行う複雑な反復作業である。同じ荷物を扱う場合でも、作業者の姿勢や動作あるいは持ち方に微妙に差が生じる。そこには単純な人の試行誤差といえるものから、作業条件の誤差、それに反復による疲労に対応した動作の局所あるいは全体の最適化に応じた変化などが含まれる。MMHの作業限界を生体力学モデルや生理学モデルで理論的に求める方法もあるが、そこで考慮できる変数やばらつきには限りがある。どうしても実際に人が作業を行う作業実験(心理物理学に基づく実験)との一貫性を確認する必要がある。
ただし実測実験は、実際に人に反復するMMH作業をしてもらうことになるので、膨大な時間と手間がかかる。この高いハードルを果敢に乗り越えて多数の実験参加者の実測データを何十年もかけて集め、整理・公表されたのがSnook & Ciriello Tables(Snook tablesあるいはLiberty Mutual tablesとも呼ばれる)である。1991年版のSnook & Ciriello Tablesは文献[3]に掲載されている。受容率(その作業を実施できる人の割合)で表示したLiberty Mutual tablesは、文献[4]のリンクから取得できる(ただし、インチ・ポンドの単位の表のみ)。文献[1]によると、119人に対して全部で11種類のMMHの実験を行い、各実験につき16-20時間の訓練時間をかけて1人につき80時間以上、数年かけて測定したとある。
初版のTable[2]は1978年にリリースされ、その後もデータの追加などが行われて、現在広く利用されているものは1991年のバージョン[3]である。初版のデータ収集は1967年に開始されており、1991年版までの間に実に24年間かけている。
Snook & Ciriello Tablesは、荷物の持ち上げ、運搬、押し引きというMMHの代表的な作業について、作業条件に応じて、男女別・対象集団の受容率ごとに値が集計されたものである。表を引けば簡単に値が直読できるだけでなく、何よりも実データに基づく値であることから、世界中で広く利用された。のちに開発されたNIOSH lifting equation (NLE)、HSEのMAC、ISO 11228-2でも、Snook & Ciriello Tablesはそのバックデータとして利用されている。
本稿で解説するLM-MMHの式は、表の形で整理されていたSnook & Ciriello Tablesを数式で表現できるように再整理したものである。その際、新たに多くの実験参加者のデータを加えてより信頼性を上げている(参加者数は、1991年版では119人だったが、LM-MMHでは273人)[1]。Snook & Ciriello Tablesでは作業条件がカテゴリで与えられていたので、利用者は必要に応じて近傍の値から線形補間でより近い値を求める必要があった。このような作業は、LM-MMHの式をPCで利用することにより格段に簡素化された。1991年版のSnook & Ciriello TablesとLM-MMHの式との値の差は、受容率50%の値で全条件を比較したところ、女性で6.7% (2.5 kg)、男性で4.8% (4.6 kg) とされている(詳細は文献[1]のTable 4を参照のこと)。今後は、Snook & Ciriello Tablesに代わってLM-MMHの式が利用されるようになると思われる。
【3】LM-MMHの式の概要
・LM-MMHでは、荷物の持ち上げ・持ち下げ、荷物の運搬、台車等の押し・引きの3種類の作業について、それぞれの作業条件での最大許容荷重(MAL: Maximum Acceptable Load)を求める。作業はいずれも両手での作業に限定されている。
・MALの平均値であるMAL50(50パーセンタイル値)は、参照質量RL (Reference Load) に複数のスケールファクターSFiをかけた式で求められる。スケールファクターSFiは、作業条件を1以下の乗数に変換したものである。各条件とも最良の場合はSFi=1、そうでない場合は1より小さな値になり、悪い条件ほど0に近い値になる。作業条件からSFiを求める式は作業種類による。
MAL50=RL×SF1×SF1×SF3×・・・
・参照質量RLとSFiの式は、男女別に決められている。また、変動係数CVも条件別・男女別に与えられている。これより、性別と対象集団の受容率に応じたMALを求める。
・Snook & Ciriello Tablesでは、持ち上げの作業条件として荷物のサイズ(横幅)があったが、LM-MMHの式ではMALへの寄与が小さいということで省かれている。
【4】持ち上げ・持ち下げ
1.入力項目
1)始点の水平距離H[m]
左右の足首の中点から両手の握りの中点までの水平距離を入力する。男性は0.25~0.73 m、女性は0.20~0.68 mの範囲で指定する。最小値は体との干渉、最大値は手の水平リーチによる範囲である。手の水平距離が左右で異なるときは、平均距離を使う。持ち上げの始点と終点で距離が異なるときは平均値か最大値を使う。
2)始点の高さV[m]
持ち上げの時は、床面(0 m)から手を上に伸ばした時の最大リーチ-0.25 mの範囲で指定する。0.25 mは持ち上げ高さDVの最小幅である。持ち下げ(降ろし)の時は、手を上に伸ばした時のリーチから床上0.25 mの範囲で指定する。LM-MMHでは、手を上に伸ばした最も高い位置は男性では2.14 m、女性では1.96 mとされている(いずれも男女の50パーセンタイル値による)。
3)上げ下げ高さDV[m]
荷物を持ち上げるあるいは下す幅を指定する(いずれも正の値で指定)。持ち上げの場合、最小は0.25 m、最大は手を上に伸ばした時の最大リーチである。持ち下げの場合は、最小値は0.25 m、最大値は始点の高さVである。本手法では、始点と始点で高さの差がない持ち上げ(つまりDV=0 m)の評価はできない。
4)反復頻度F[回/分]
1分間あたりの持ち上げの繰り返し回数で指定する。最小値は1/480 回/分、最大値は20 回/分である。最小値は1日の8時間の労働時間内で1回(8時間×60分=480分)の意味である。最大値は20[回/分]であるが、平均移動速度(=DV×F)が11 m/分を越えない範囲に限定される。
5)荷物の持ちやすさの補正係数(Coupling scale factor)
取手のない場合は0.84、不良なハンドルしかない場合や滑りやすい場合は0.925をそれぞれMALにかける。

2.各変数の参照質量RL、スケールファクターSFへの変換式、変動係数CV
H: 水平距離 [m]
V: 始点高さ [m]
DV: 上げ下げ高さ [m]
F: 反復頻度 [回/分]
上変数より、平均高さVRMを求めておく:
VRM = V + DV/2 持ち上げ時
VRM = V – DV/2 持ち下げ時
MAL50の式は以下の通り:
MAL50 = RL × HSF × VRMSF × DVSF × FSF × CSF
ここで、
RL: 参照質量
HSF: 水平距離スケールファクター
VRMSF: 平均高さスケールファクター
DVSF: 上げ下げ高さスケールファクター
FSF: 反復頻度スケールファクター
CSF: ハンドル持ちやすさスケールファクター
各条件別のRL等は以下の通り:
(注1)Ln( )は自然対数の関数である
(注2)スケールファクターの計算値が1を超える場合は1とする。
1)持ち上げ・女性
RL = 34.9
HSF = (1.2602 – H/0.7686)
VRMSF = (0.9877 + VRM/13.69 – VRM2/9.221)
DVSF = (0.8199 – Ln(DV)/7.696)
FSF = (0.6767 – Ln(F)/12.59 – Ln(F)2/228.2)
CV = 0.26
2)持ち上げ・男性
RL = 82.6
HSF = 1.3532 – H/0.7079
VRMSF = 0.7746 + VRM/1.912 – VRM2/3.296
DVSF = 0.8695 – Ln(DV)/10.62
FSF = 0.6259 – Ln(F)/9.092 – Ln(F)2/125.0
CV = 0.276
3)持ち下げ・女性
RL = 37.0
HSF = 1.2602 – H/0.7686
VRMSF = 0.9877 + VRM/13.69 – VRM2/9.221
DVSF = 0.8199 – Ln(DV)/7.696
FSF = 0.6767 – Ln(F)/12.59 – Ln(F)2/228.2
CV = 0.307
4)持ち下げ・男性
RL = 95.9
HSF = 1.3532 – H/0.7079
VRMSF = 0.7746 + VRM/1.912 – VRM2/3.296
DVSF = 0.8695 – Ln(DV)/10.62
FSF = 0.5773 – Ln(F)/10.80 – Ln(F)2/255.9
CV = 0.304
5)ハンドル結合(男女・持ち上げ持ち下げ共通)
CSF = 1 良好
CSF = 0.84 不良
CSF = 0.925 なし
(持ち上げ・持ち下げのスケールファクターのグラフ)
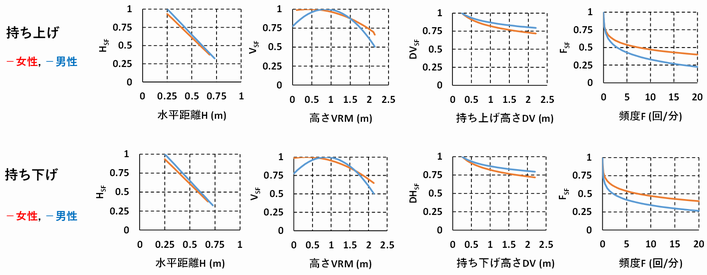
【5】運搬
1.入力項目
1)手の高さV[m]
運搬中の手の握りの床からの高さ(左右の中点)を指定する。値の範囲は、男性では0.78-1.10 m、女性では0.71-1.03 mに限定されている。
2)運搬距離DH[m]
運搬の始点から終点への手位置(左右の中点)の水平距離を指定する。距離は2.1-10 mの範囲に制限されている。
3)反復頻度F[回/分]
1分間あたりの運搬の繰り返し回数で指定する。最小値は1/480 回/分、最大値は10 回/分である。最小値は1日の8時間の労働時間内で1回(8時間×60分=480分)の意味である。最大値は10[回/分]であるが、平均移動速度(=DH×F)が29 m/分を越えない範囲に限定される。
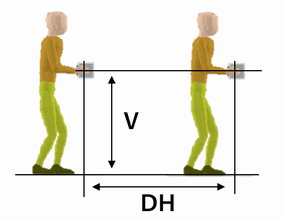
2.各変数の参照質量RL、スケールファクターSFへの変換式、変動係数CV
V: 手の高さ [m]
DH: 移動距離 [m]
F: 反復頻度 [回/分]
MAL50の式は以下の通り:
MAL50 = RL × VSF × DHSF × FSF
ここで、
RL: 参照質量
VSF: 手の高さスケールファクター
DHSF: 移動距離スケールファクター
FSF: 反復頻度スケールファクター
各条件別のRL等は以下の通り:
(注1)Ln( )は自然対数の関数である
(注2)スケールファクターSFの計算値が1を超える場合は1とする。
1)女性
RL = 28.6
VSF = 1.1645 – V/4.437
DHSF = 1.0101 – DH/207.8
FSF = 0.6224 – Ln(F)/16.33
CV = 0.231
2)男性
RL = 74.9
VSF = 1.5505 – V/1.417
DHSF = 1.1172 – Ln(DH)/6.332
FSF = 0.5149 – Ln(F)/7.958 – Ln(F)2/131.1
CV = 0.278
(運搬のスケールファクターのグラフ)
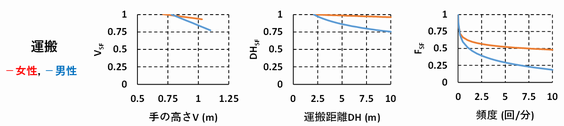
【6】台車等の押し引き
1.入力項目
1)ハンドルの高さV[m]
台車のハンドルの握りの床からの高さ(左右の中点)を指定する。値の範囲は、男性では0.63-1.44 m、女性では0.58-1.33 mに限定されている。
2.運搬距離DH[m]
運搬の始点から終点への手位置(左右の中点)の水平距離を指定する。距離は2.1-61 mの範囲に制限されている。
3.反復頻度F[回/分]
1分間あたりの運搬の繰り返し回数で指定する。最小値は1/480 回/分、最大値は10 回/分である。最小値は1日の8時間の労働時間内で1回(8時間×60分=480分)の意味である。最大値は10 回/分であるが、平均移動速度(=DH×F)が37 m/分を越えない範囲に限定される。
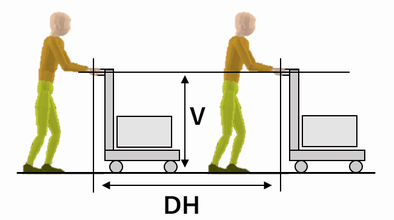
2.各変数の参照質量RL、スケールファクターSFへの変換式、変動係数CV
押し引きには、初期の押し力 (Initial force)と維持の押し力 (Sustained force) の2種類がある。前者の初期押し力は、台車等を押してスタートする初期の加速時の力発揮、後者は台車等が一定の速度で動いている途中で維持する力発揮のことである。
V: ハンドル高さ [m]
DH: 移動距離 [m]
F: 反復頻度 [回/分]
MAL50の式は以下の通り:
MAL50 = RL × VSF × DHSF × FSF
ここで、
RL: 参照質量
VSF: ハンドル高さスケールファクター
DHSF: 移動距離スケールファクター
FSF: 反復頻度スケールファクター
各条件別のRL等は以下の通り:
(注1)Ln( )は自然対数の関数である
(注2)スケールファクターの計算値が1を超える場合は1とする。
1)女性・押し
(1)初期力
RL = 36.9
VSF = -0.5304 + V/0.3361 – V2/0.6915
DHSF = 1.0286 – DH/72.22 + DH2/ 9782
FSF = 0.7251 – Ln(F)/13.19 – Ln(F)2/197.3
CV = 0.214
(2)維持力
RL = 25.5
VSF = -0.6539 + V/0.2941 – V2/0.5722
DHSF = 1.0391 – DH/52.91 + DH2/7975
FSF = 0.6086 – Ln(F)/11.95 – Ln(F)2/304.4
CV = 0.286
2)女性・引き
(1)初期力: CV除き、女性・押しと同じ
RL = 36.9
VSF = -0.5304 + V/0.3361 – V2/0.6915
DHSF = 1.0286 – DH/72.22 + DH2/9782
FSF = 0.7251 – Ln(F)/13.19 – Ln(F)2/197.3
CV = 0.234
(2)維持力:CV除き、女性・押しと同じ
RL = 25.5
VSF = -0.6539 + V/0.2941 – V2/0.5722
DHSF = 1.0391 – DH/52.91 + DH2/7975
FSF = 0.6086 – Ln(F)/11.95 – Ln(F)2/304.4
CV = 0.298
3)男性・押し
(1)初期力
RL = 70.3
VSF = 1.2737 – V/1.335 + V2/2.576
DHSF = 1.079 – Ln(DH)/9.392
FSF = 0.6281 – Ln(F)/13.07 – Ln(F)2/379.5
CV = 0.231
(2)維持力
RL = 65.3
VSF = 2.294 – V/0.3345 + V2/0.6887
DHSF = 1.1035 – Ln(DH)/7.17
FSF = 0.4896 – Ln(F)/10.20 – Ln(F)2/403.9
CV = 0.267
4)男性・引き
(1)初期力
RL = 69.8
VSF = 1.7186 – V/0.6888 + V2/2.025
DHSF = 1.079 – Ln(DH)/9.392
FSF = 0.6281 – Ln(F)/13.07 – Ln(F)2/379.5
CV = 0.238
(2)維持力
RL = 61.0
VSF = 2.1977 – V/0.385 + V2/0.9047
DHSF = 1.1035 – Ln(DH)/7.17
FSF = 0.4896 – Ln(F)/10.20 – Ln(F)2/403.9
CV = 0.257
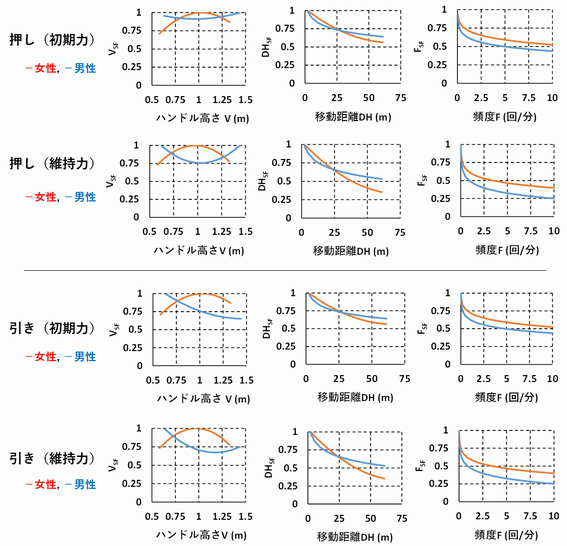
(押し引きのスケールファクターのグラフ)
【7】対象集団の受容率に応じたMALの算出
前項の式で求めたMAL50は、指定された性別の作業者が指定された作業条件で取り扱うことのできる荷物質量上限の50パーセンタイル値である。MAL50をそのまま荷物質量に採用すると、対象集団の半分の人しか作業できない状態になる。そこで本法では、MALが平均値MAL50、標準偏差CV×MAL50の正規分布に従うと仮定して、対象集団の受容率AC (Acceptability)に応じたMAL(パーセンタイル値)を求める。ここでの受容率ACとは、対象集団の何パーセントの人が取り扱い可能かという値である。
受容率AC[%]のMAL(AC[%]の人が作業できるMAL)は、MALが平均値MAL50、標準偏差CV×MAL50の正規分布に従うとすると、その上側累積確率がAC[%]の値(あるいは下側累積確率が100%-ACの値)に該当する。エクセルの正規分布の関数NORM.INV()を使うと、以下の式で求められる:
MAL=NORM.INV(1-AC/100, MAL50, CV×MAL50).
NORM.INV()は、平均値m, 標準偏差sdの正規分布するデータXの下側累積確率がpとなる値Xpを求めるエクセルの関数である。
Xp=NORM.INV(p, m, sd)
標準正規分布の下側累積確率pの値を求めるエクセルの関数NORM.S.INV(p)を使う場合は、以下のように表せる:
MAL=MAL50+NORM.S.INV(1-AC/100)×CV×MAL50.
(例題)
MALの平均値MAL50が20 kg, 変動係数CVが0.25の場合、受容率ACが75%のMALの値を求める。
標準正規分布の上側累積確率がAC[%]の値は次の取り:
NORM.S.INV(1-AC/100)=NORM.S.INV(1-75/100)
=NORM.S.INV(0.25)=-0.67449.
従って、受容率ACが75%のMALは次の通り:
MAL=MAL50+NORM.S.INV(1-AC/100)×CV×MAL50
=20+(-0.67449)×0.25×20
=16.6 kg.
受容率ACとして、本法の解説論文[4]では、経験的に女性の受容率75%を使用するのが妥当と述べられている。後述するように本法を参照した他のツールでは、NLEは女性の受容率75%、HSEは女性の受容率50%に相当する値を荷物質量上限としている。
【8】使用法など
1.該当するMMHについて、性別や対象集団の受容率を決め、必要な変数データを得て、各式を利用してスケールファクター等を求め、MALを計算する。
2.実作業で取り扱い荷物や押し引き力とMALを比較して評価する。MALは想定する対象集団の受容率に対して求められるので、受容率を変えれば判定も変わる。受容率が高い、つまりあらゆる対象者がカバーできる条件ほど、MALは小さくなる。逆に受容率が低い、つまり特定の対象者のみ対応できる条件であるほど、MALは大きくなる。想定した作業の荷物質量が、想定した対象集団の受容率でのMALを下回るなら、作業は安全に実現できることになる。
3.作業条件がMALに与える影響の程度は、スケールファクターSFで判断する。つまり、SFが1に近い変数はMALの低下を引き起こさない良い条件であり、1より小さいSFはMALの低下を引き起こしやすいよくない条件とみなされる。つまり改善すべき作業条件といえる。このように、SFの小さいものから改善をすると、効果的に改善を進めることができ、かつ、改善によるMALの増加が実作業に見合うかどうかの判定もできる。
4.国内の荷物取り扱い作業は、「職場における腰痛予防対策指針」で男性の手作業での荷重は体重の40%まで(女性は男性の60%まで)とされている。本式で計算すると特に男性でそれをはるかに超える値が示される場合がある。それに対して、NLEでは女性の受容率75%、HSEでは女性の受容率50%、ISO 11228-2では女性の受容率90%の値を男女混成の作業者集団での低リスクと判断する基準値として参照している。前述したように、本法の解説論文[4]では、経験的には女性の受容率75%の値を満たすように作業設計するのがよいと述べられている。女性の受容率75%の値でも、すべてのスケールファクターが1になる条件でのMALは持ち上げ・持ち下げで29 kg、運搬で24 kgとなり、国内指針の女性への適用値としてはまだ高い。ただし実際のスケールファクターが1にならない現実的な作業条件だと、多くの場合で15 kg前後の値にはなる。これを参考に、女性の受容率75%をMAL設定の一つの目安にするとよい。
【9】その他
- 本式で想定されている体格は、男性は身長1.79 m、女性は1.63 mである [1]。
- LM-MMHの式での値は、あくまで両手作業で体のひねりのない快適な作業環境での値である。持ち上げに関しては、上述したようにハンドルの状況Cに応じたスケールファクターCSFがあるが、その他の作業要因(ひねり、作業時間、片手など)は考慮されてない。この点を拡張して適用範囲を広げたのが、NLEやISO 11228-1, 11228-2などの評価法である。
- 押し引き力の初期力と維持力の測定法については、文献[1]~[3]には特に明記はないが、ISO 11228-2:2007のAnnex Dに詳しい測定法が記載されている。同ISOは押し引き力のMMHの規格であるが、最初のスクリーニングの段階ではSnook Tablesの押し引き力の表を参照している。
文献
[1] Jim R. Potvin, Vincent M. Ciriello, Stover H. Snook, Wayne S. Maynard and George E. Brogmus, “The Liberty Mutual manual materials handling (LM-MMH) equations”, Ergonomics, 64, 8, pp.955-970,2021, doi: 10.1080/00140139.2021.1891297
[2] Snook, S.H., “The design of manual handling tasks”, Ergonomics, 21, 12, pp.963-985, 1978, doi: 10.1080/00140137808931804.
[3] Snook, S.H. and V.M. Ciriello, “The design of manual handling tasks: revised tables of maximum acceptable weights and forces”, Ergonomics, 34, 9, pp.1197-1213, 1991, doi: 10.1080/00140139108964855.
[4] Liberty Mutual, Liberty Mutual Tables, https://libertymmhtables.libertymutual.com/CM_LMTablesWeb/pdf/LibertyMutualTables.pdf